
分析 B={(x,y)|$\frac{{x}^{2}}{9}$+$\frac{{y}^{2}}{4}$≤1},表示椭圆$\frac{{x}^{2}}{9}$+$\frac{{y}^{2}}{4}$=1及其内部的点.而集合A={(x,y)|$\frac{|x|}{3}$+$\frac{|y|}{2}$≤1},表示经过椭圆$\frac{{x}^{2}}{9}$+$\frac{{y}^{2}}{4}$=1的四个顶点的四条直线及其内部的点,即可判断出结论.
解答 解:B={(x,y)|$\frac{{x}^{2}}{9}$+$\frac{{y}^{2}}{4}$≤1},表示椭圆$\frac{{x}^{2}}{9}$+$\frac{{y}^{2}}{4}$=1及其内部的点.而集合A={(x,y)|$\frac{|x|}{3}$+$\frac{|y|}{2}$≤1},表示经过椭圆$\frac{{x}^{2}}{9}$+$\frac{{y}^{2}}{4}$=1的四个顶点的四条直线及其内部的点,
则命题“p:(x,y)∈A”是命题“q:(x,y)∈B”的“充分不必要”条件.
故答案为:充分不必要
点评 本题考查了椭圆与直线的方程、不等式的解集、简易逻辑的判定方法,考查了推理能力与计算能力,属于中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{3}{4}$ | B. | $\frac{4}{3}$ | C. | $\frac{4}{5}$ | D. | $\frac{5}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
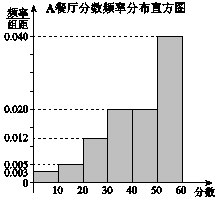 某大学为调研学生在A,B两家餐厅用餐的满意度,从在A,B两家餐厅都用过餐的学生中随机抽取了100人,每人分别对这两家餐厅进行评分,满分均为60分.整理评分数据,将分数以10为组距分成6组:[0,10),[10,20),[20,30),[30,40),[40,50),[50,60],得到A餐厅分数的频率分布直方图,和B餐厅分数的频数分布表:
某大学为调研学生在A,B两家餐厅用餐的满意度,从在A,B两家餐厅都用过餐的学生中随机抽取了100人,每人分别对这两家餐厅进行评分,满分均为60分.整理评分数据,将分数以10为组距分成6组:[0,10),[10,20),[20,30),[30,40),[40,50),[50,60],得到A餐厅分数的频率分布直方图,和B餐厅分数的频数分布表:| B餐厅分数频数分布表 | |
| 分数区间 | 频数 |
| [0,10) | 2 |
| [10,20) | 3 |
| [20,30) | 5 |
| [30,40) | 15 |
| [40,50) | 40 |
| [50,60] | 35 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{2017}{2018}$ | B. | $\frac{2014}{2015}$ | C. | $\frac{2015}{2016}$ | D. | $\frac{2016}{2017}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{5}$ | B. | $\frac{1}{2}$ | C. | $\frac{{2\sqrt{6}}}{5}$ | D. | $\frac{{\sqrt{3}}}{5}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com