
分析 由已知得圆心C(-1,-1)在直线ax+by+4=0上,从而b=-a+4,点(a,b)向圆所作的切线长为:$\sqrt{(a+1)^{2}+(b+1)^{2}-9}$=$\sqrt{2(a-2)^{2}+9}$,由此能求出点(a,b)向圆所作的切线长的最小值.
解答 解:∵圆C:x2+y2+2x+2y-7=0可化简为:(x+1)2+(y+1)2=9
∴圆C的圆心为(-1,1),半径r=3
∵圆C:x2+y2+2x+2y-7=0关于直线ax+by+4=0对称,
∴圆心C(-1,-1)在直线ax+by+4=0上,
∴-a-b+4=0,即b=-a+4,
点(a,b)向圆所作的切线长为:$\sqrt{(a+1)^{2}+(b+1)^{2}-9}$=$\sqrt{2(a-2)^{2}+9}$,
∴当a=2时,点(a,b)向圆所作的切线长取得最小值3.
故答案为3.
点评 本题考查切线长的最小值的求法,是中档题,解题时要认真审题,注意圆的性质、两点间距离公式的合理运用.


 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南大学出版社系列答案
同步练习西南大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案科目:高中数学 来源: 题型:解答题
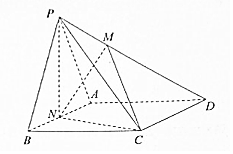 如图,在四棱锥P-ABCD中,底面ABCD为菱形,∠ABC=60°,PA=PB=AB=2,点N为AB的中点.,
如图,在四棱锥P-ABCD中,底面ABCD为菱形,∠ABC=60°,PA=PB=AB=2,点N为AB的中点.,查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (1,$\frac{{2\sqrt{3}}}{3}$) | B. | (1,2) | C. | (2,+∞) | D. | ($\frac{{2\sqrt{3}}}{3}$,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 车牌尾号 | 0和5 | 1和6 | 2和7 | 3和8 | 4和9 |
| 限行日 | 星期一 | 星期二 | 星期三 | 星期四 | 星期五 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | c>b>a | B. | c>a>b | C. | b>a>c | D. | a>b>c |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com