练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    9．设i是虚数单位，$\overline z$是复数z的共轭复数，若$z=\frac{2}{-1+i}$，则$\overline z$=（　　）
    A．1-iB．1+iC．-1-iD．-1+i

    分析 利用复数代数形式的乘除运算化简，再由共轭复数的概念得答案．

    解答 解：∵$z=\frac{2}{-1+i}$=$\frac{2（-1-i）}{（-1+i）（-1-i）}=\frac{2（-1-i）}{2}=-1-i$，
    ∴$\overline{z}=-1+i$．
    故选：D．

    点评 本题考查复数代数形式的乘除运算，考查复数的基本概念，是基础的计算题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：填空题

    19．已知sinθ+2cosθ=0，则$\frac{1+sin2θ}{{{{cos}^2}θ}}$=1．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

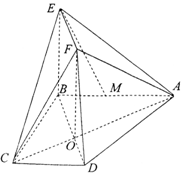    20．如图所示，梯形ABCD两条对角线AC，BD的交点为O，AB=2CD，四边形OBEF为矩形，M为线段AB上一点，AM=2MB．
    （Ⅰ）求证：EM∥平面ADF；
    （Ⅱ）若EF⊥CF，求证AC⊥BD．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

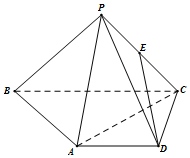    17．在四棱锥P-ABCD中，AD∥BC，AD=AB=DC=$\frac{1}{2}$BC=1，E是PC的中点，面PAC⊥面ABCD．
    （Ⅰ）证明：ED∥面PAB；
    （Ⅱ）若PC=2，PA=$\sqrt{3}$，求二面角A-PC-D的余弦值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    4．已知f（x）为定义在$（0，\frac{π}{2}）$上的函数，f'（x）是它的导函数，且$\frac{f'（x）}{tanx}＜f（x）$恒成立，则（　　）
    A．$f（\frac{π}{3}）＜\sqrt{3}f（\frac{π}{6}）$B．$f（\frac{π}{6}）＜\sqrt{2}f（\frac{π}{4}）$C．$f（\frac{π}{3}）＜f（\frac{π}{4}）$D．$f（\frac{π}{4}）＜\sqrt{3}f（\frac{π}{3}）$

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    14．已知集合M={x|$\frac{{x}^{2}}{9}$+$\frac{{y}^{2}}{4}$=1}，N={y|$\frac{x}{3}$+$\frac{y}{2}$=1}，M∩N=（　　）
    A．∅B．{（3，0），（0，2）}C．[一2，2]D．[一3，3]

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

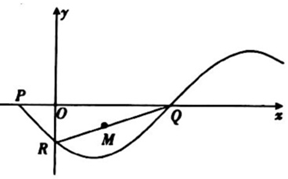    1．如图，函数f（x）=Asin（ωx+φ）（A＞0，ω＞0，|φ|＜π）的部分图象与坐标轴的三个交点分别为P（-1，0），Q、R，且线段RQ的中点M的坐标为（$\frac{3}{2}$，-$\frac{1}{2}$），则f（-2）等于（　　）
    A．1B．-1C．$\frac{\sqrt{6}}{2}$D．-$\frac{\sqrt{6}}{2}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

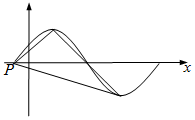    18．已知函数$f（x）=sin2x+sin（\frac{π}{3}-2x）$．
    （Ⅰ）求f（x）的最大值及相应的x值；
    （Ⅱ）设函数$g（x）=f（\frac{π}{4}x）$，如图，点P，M，N分别是函数y=g（x）图象的零值点、最高点和最低点，求cos∠MPN的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    19．已知函数h（x）=（x-a）ex+a．
    （1）若x∈[-1，1]，求函数h（x）的最小值；
    （2）当a=3时，若对?x1∈[-1，1]，?x2∈[1，2]，使得h（x1）≥x22-2bx2-ae+e+$\frac{15}{2}$成立，求b的范围．

    查看答案和解析>>

    同步练习册答案