
分析 (1)求出极值点x=a-1.通过当a≤0时,当0<a<2时,当a≥2时,利用函数的单调性求解函数的最小值.
(2)令$f(x)={x^2}-2bx-ae+e+\frac{15}{2}$,“对?x1∈[-1,1],?x2∈[1,2],使得$h({x_1})≥{x_2}^2-2b{x_2}-ae+e+\frac{15}{2}$成立”等价于“f(x)在[1,2]上的最小值不大于h(x)在[-1,1]上的最小值”.推出h(x)min≥f(x)min.通过①当b≤1时,②当1<b<2时,③当b≥2时,分别利用极值与最值求解b的取值范围.
解答 解:(1)h'(x)=(x-a+1)ex,令h'(x)=0得x=a-1.
当a-1≤-1即a≤0时,在[-1,1]上h'(x)≥0,函数h(x)=(x-a)ex+a递增,h(x)的最小值为$h(-1)=a-\frac{1+a}{e}$.
当-1<a-1<1即0<a<2时,在x∈[-1,a-1]上h'(x)≤0,h(x)为减函数,在x∈[a-1,1]上h'(x)≥0,h(x)为增函数.∴h(x)的最小值为h(a-1)=-ea-1+a.
当a-1≥1即a≥2时,在[-1,1]上h'(x)≤0,h(x)递减,h(x)的最小值为h(1)=(1-a)e+a.
综上所述,当a≤0时h(x)的最小值为$a-\frac{1+a}{e}$,当a≥2时h(x)的最小值为(1-a)e+a,当0<a<2时,h(x)最小值为-ea-1+a.
(2)令$f(x)={x^2}-2bx-ae+e+\frac{15}{2}$,
由题可知“对?x1∈[-1,1],?x2∈[1,2],使得$h({x_1})≥{x_2}^2-2b{x_2}-ae+e+\frac{15}{2}$成立”
等价于“f(x)在[1,2]上的最小值不大于h(x)在[-1,1]上的最小值”.
即h(x)min≥f(x)min.
由(1)可知,当a=3时,h(x)min=h(1)=(1-a)e+a=-2e+3.
当a=3时,$f(x)={x^2}-2bx-2e+\frac{15}{2}={(x-b)^2}-{b^2}-2e+\frac{15}{2}$,x∈[1,2],
①当b≤1时,$f{(x)_{min}}=f(1)=-2b-2e+\frac{17}{2}$,
由$-2e+3≥-2b-2e+\frac{17}{2}$得$b≥\frac{11}{4}$,与b≤1矛盾,舍去.
②当1<b<2时,$f{(x)_{min}}=f(b)=-{b^2}-2e+\frac{15}{2}$,
由$-2e+3≥-{b^2}-2e+\frac{15}{2}$得${b^2}≥\frac{9}{2}$,与1<b<2矛盾,舍去.
③当b≥2时,$f{(x)_{min}}=f(2)=-4b-2e+\frac{23}{2}$,
由$-2e+3≥-4b-2e+\frac{23}{2}$得$b≥\frac{17}{8}$.
综上,b的取值范围是$[{\frac{17}{8},+∞})$.
点评 本题考查函数的导数的综合应用,函数的极值以及函数的单调性与函数的最值的关系,考查分析问题解决问题的能力.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | 1-i | B. | 1+i | C. | -1-i | D. | -1+i |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
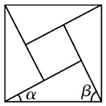 《周髀算经》中给出了弦图,所谓弦图是由四个全等的直角三角形和中间一个小正方形拼成一个大的正方形,若图中直角三角形两锐角分别为α、β,且小正方形与大正方形面积之比为4:9,则cos(α-β)的值为( )
《周髀算经》中给出了弦图,所谓弦图是由四个全等的直角三角形和中间一个小正方形拼成一个大的正方形,若图中直角三角形两锐角分别为α、β,且小正方形与大正方形面积之比为4:9,则cos(α-β)的值为( )| A. | $\frac{5}{9}$ | B. | $\frac{4}{9}$ | C. | $\frac{2}{3}$ | D. | 0 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{8}{25}$ | B. | $\frac{16}{25}$ | C. | $\frac{49}{100}$ | D. | $\frac{49}{200}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -36 | B. | -9 | C. | 9 | D. | 36 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
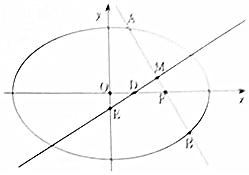 过椭圆C:$\frac{{x}^{2}}{2}$+y2=1的右焦点F的直线l交椭圆于A,B两点,M是AB的中点.
过椭圆C:$\frac{{x}^{2}}{2}$+y2=1的右焦点F的直线l交椭圆于A,B两点,M是AB的中点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com