
���� ��1���������ַ��̵�ת��������������C����ͨ������ֱ��l��ֱ�����귽�̣�
��2�������⣬Բ�ĵ�ֱ�ߵľ���d=$\sqrt{16-4}$=2$\sqrt{3}$��������ʵ��m��ֵ��
��� �⣺��1������C�IJ�������Ϊ$\left\{\begin{array}{l}{x=1+4cos��}\\{y=-1+4sin��}\end{array}\right.$����Ϊ����������ͨ����Ϊ��x-1��2+��y+1��2=16��
ֱ��l��$��=\frac{2\sqrt{2}m}{sin����+\frac{��}{4}��}$������sin��+��cos��=4m��ֱ�����귽��Ϊx+y-4m=0��
��2�������⣬Բ�ĵ�ֱ�ߵľ���d=$\sqrt{16-4}$=2$\sqrt{3}$��
��$\frac{|-4m|}{\sqrt{2}}$=2$\sqrt{3}$����m=��$\frac{\sqrt{6}}{2}$��
���� ���⿼�����ַ��̵�ת��������ֱ����Բ��λ�ù�ϵ�������ҳ��ļ��㣬�����е��⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $f��\frac{��}{3}����\sqrt{3}f��\frac{��}{6}��$ | B�� | $f��\frac{��}{6}����\sqrt{2}f��\frac{��}{4}��$ | C�� | $f��\frac{��}{3}����f��\frac{��}{4}��$ | D�� | $f��\frac{��}{4}����\sqrt{3}f��\frac{��}{3}��$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | [1��e] | B�� | $��{1+\frac{1}{e}��e}]$ | C�� | ��0��e] | D�� | $[{1+\frac{1}{e}��e}]$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
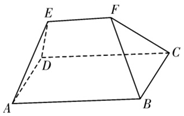 �й��Ŵ���ѧ�������������������м��أ���ۻ���ߣ��������й㣬���������㣮ۻ����Ҳ�������ݸ�Ҳ��������Ϊ�������г��п�Ϊ���Σ�����ֻ�г�û�п�Ϊһ���⣮ۻ��������˼Ϊé���ݶ���������һ��ۻ����ͼ��ʾ���ı���ABCDΪ�����Σ��ı���ABFE��CDEFΪ����ȫ�ȵĵ������Σ�AB=4��EF$\underset{��}{=}$$\frac{1}{2}$AB�������ۻ�������Ϊ$\frac{40}{3}$��������ֱ��AB��CF���ɽǵ�����ֵΪ��������
�й��Ŵ���ѧ�������������������м��أ���ۻ���ߣ��������й㣬���������㣮ۻ����Ҳ�������ݸ�Ҳ��������Ϊ�������г��п�Ϊ���Σ�����ֻ�г�û�п�Ϊһ���⣮ۻ��������˼Ϊé���ݶ���������һ��ۻ����ͼ��ʾ���ı���ABCDΪ�����Σ��ı���ABFE��CDEFΪ����ȫ�ȵĵ������Σ�AB=4��EF$\underset{��}{=}$$\frac{1}{2}$AB�������ۻ�������Ϊ$\frac{40}{3}$��������ֱ��AB��CF���ɽǵ�����ֵΪ��������| A�� | $\frac{1}{3}$ | B�� | $\frac{2}{3}$ | C�� | $\frac{\sqrt{5}}{3}$ | D�� | $\frac{2\sqrt{2}}{3}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{1}{5}$ | B�� | $\frac{2}{5}$ | C�� | $\frac{3}{5}$ | D�� | $\frac{4}{5}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com