
分析 根据题意画出图形,结合图形,设外接圆的半径为r,对$\overrightarrow{OM}$=p$\overrightarrow{OB}$+q$\overrightarrow{OC}$两边平方,建立p、q的解析式,利用基本不等式求出p+q的取值范围.
解答 解:如图所示,△ABC中,∠A=$\frac{π}{3}$,∴∠BOC=$\frac{2π}{3}$;
设|$\overrightarrow{OA}|=|\overrightarrow{OB}|=|\overrightarrow{OC}$=r,则O为△ABC外接圆圆心;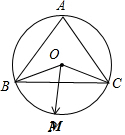
∵$\overrightarrow{OM}$=p$\overrightarrow{OB}$+q$\overrightarrow{OC}$,
∴${|\overrightarrow{OM}|}^{2}$=${(p\overrightarrow{OB}+q\overrightarrow{OC})}^{2}$=r2,
即p2r2+q2r2+2pqr2cos$\frac{2π}{3}$=r2,
∴p2+q2-pq=1,
∴(p+q)2=3pq+1;
又M为劣弧AC上一动点,
∴0≤p≤1,0≤q≤1,
∴p+q≥2$\sqrt{pq}$,
∴pq≤${(\frac{p+q}{2})}^{2}$=$\frac{{(p+q)}^{2}}{4}$,
∴1≤(p+q)2≤$\frac{3}{4}$(p+q)2+1,
解得1≤(p+q)2≤4,
∴1≤p+q≤2;
即p+q的取值范围是[1,2].
故答案为:[1,2].
点评 本题考查了平面向量的应用问题和圆周角与圆心角的关系以及基本不等式的应用问题,是综合题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
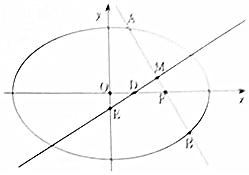 过椭圆C:$\frac{{x}^{2}}{2}$+y2=1的右焦点F的直线l交椭圆于A,B两点,M是AB的中点.
过椭圆C:$\frac{{x}^{2}}{2}$+y2=1的右焦点F的直线l交椭圆于A,B两点,M是AB的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
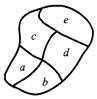 某社区新建了一个休闲小公园,几条小径将公园分成5块区域,如图,社区准备从4种颜色不同的花卉中选择若干种种植在各块区域,要求每个区域随机用一种颜色的花卉,且相邻区域(用公共边的)所选花卉颜色不能相同,则不同种植方法的种数共有( )
某社区新建了一个休闲小公园,几条小径将公园分成5块区域,如图,社区准备从4种颜色不同的花卉中选择若干种种植在各块区域,要求每个区域随机用一种颜色的花卉,且相邻区域(用公共边的)所选花卉颜色不能相同,则不同种植方法的种数共有( )| A. | 96 | B. | 114 | C. | 168 | D. | 240 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
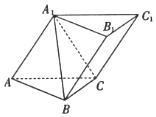 如图,在三棱锥ABC-A1B1C1中,侧面ACC1A1⊥底面ABC,△A1AC为等边三角形,AC⊥A1B.
如图,在三棱锥ABC-A1B1C1中,侧面ACC1A1⊥底面ABC,△A1AC为等边三角形,AC⊥A1B.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 价格x(百元) | 4 | 5 | 6 | 7 | 8 | 9 |
| 销量y(件/天) | 90 | 84 | 83 | 80 | 75 | 68 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com