
分析 (1)求出函数的导数,问题转化为关于x的方程$-b=\frac{x}{e^x}$有两个不同的解,令$g(x)=\frac{x}{e^x}$,则$g'(x)=\frac{1-x}{e^x}$,根据函数的单调性求出b的范围即可;
(2)问题转化为g(x2)-g(2-x2)>0,即${e^2}{x_2}-{e^{2{x_2}}}({2-{x_2}})>0$,令h(t)=e2t-e2t(2-t),根据函数的单调性得到h(t)>0,从而证出结论.
解答 解:(1)函数f(x)的定义域为R,f'(x)=x+bex.
因为函数f(x)有两个极值点x1,x2,所以f'(x)=x+bex有两个变号零点,
故关于x的方程$-b=\frac{x}{e^x}$有两个不同的解,
令$g(x)=\frac{x}{e^x}$,则$g'(x)=\frac{1-x}{e^x}$,
当x∈(-∞,1)时g'(x)>0,当x∈(1,+∞)时,g'(x)<0,
所以函数$g(x)=\frac{x}{e^x}$在区间(-∞,1)上单调递增,在区间(1,+∞)上单调递减,
又当x→-∞时,g(x)→-∞;当x→+∞时,g(x)→0,且$g(1)=\frac{1}{e}$,
故$0<-b<\frac{1}{e}$,所以$-\frac{1}{e}<b<0$.
(2)不妨设x1<x2,由(1)可知,x1<1<x2,所以x1,2-x2∈(-∞,1),
因为函数$g(x)=\frac{x}{e^x}$在区间(-∞,1)上单调递增,
若x1+x2>2即x1>2-x2时,g(x1)>g(2-x2)即g(x1)-g(2-x2)>0.
又g(x1)=g(x2),所以g(x1)-g(2-x2)>0可化为g(x2)-g(2-x2)>0,
即$\frac{x_2}{{{e^{x_2}}}}-\frac{{2-{x_2}}}{{{e^{2-{x_2}}}}}>0$即${e^2}{x_2}-{e^{2{x_2}}}({2-{x_2}})>0$,
令h(t)=e2t-e2t(2-t),则h(1)=0,h'(t)=e2-e2t(3-2t),
令φ(t)=h'(t),则φ(1)=0,φ'(t)=4e2t(t-1),
当t>1时,φ'(t)>0,所以h'(x)在区间(1,+∞)上单调递增,则h'(t)>h'(1)=0,
所以h(t)在区间(1,+∞)上单调递增,h(t)>h(1)=0.证毕.
点评 本题考查了函数的单调性、最值问题,考查导数的应用以及分类讨论思想,转化思想,考查不等式的证明,是一道中档题.


科目:高中数学 来源: 题型:选择题
| A. | [1,e] | B. | $({1+\frac{1}{e},e}]$ | C. | (0,e] | D. | $[{1+\frac{1}{e},e}]$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
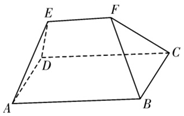 中国古代数学家名著《九章算术》中记载:“刍甍者,下有袤有广,而上有袤无广.刍,草也.甍,屋盖也.”翻译为“底面有长有宽为矩形,顶部只有长没有宽为一条棱.刍甍字面意思为茅草屋顶.”现有一个刍甍如图所示,四边形ABCD为正方形,四边形ABFE、CDEF为两个全等的等腰梯形,AB=4,EF$\underset{∥}{=}$$\frac{1}{2}$AB,若这个刍甍的体积为$\frac{40}{3}$,则异面直线AB与CF所成角的余弦值为( )
中国古代数学家名著《九章算术》中记载:“刍甍者,下有袤有广,而上有袤无广.刍,草也.甍,屋盖也.”翻译为“底面有长有宽为矩形,顶部只有长没有宽为一条棱.刍甍字面意思为茅草屋顶.”现有一个刍甍如图所示,四边形ABCD为正方形,四边形ABFE、CDEF为两个全等的等腰梯形,AB=4,EF$\underset{∥}{=}$$\frac{1}{2}$AB,若这个刍甍的体积为$\frac{40}{3}$,则异面直线AB与CF所成角的余弦值为( )| A. | $\frac{1}{3}$ | B. | $\frac{2}{3}$ | C. | $\frac{\sqrt{5}}{3}$ | D. | $\frac{2\sqrt{2}}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{5}$ | B. | $\frac{2}{5}$ | C. | $\frac{3}{5}$ | D. | $\frac{4}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com