
分析 (1)利用两角和的正弦函数公式及二倍角公式化简函数f(x),再由周期公式计算得答案;
(2)由已知条件求出g(x)=$\frac{1}{2}$sin(2x+$\frac{π}{3}$)+$\frac{1}{2}$,当x∈[-$\frac{π}{6}$,$\frac{π}{2}$]时,则2x+$\frac{π}{3}$∈$[0,\frac{4π}{3}]$,由正弦函数的值域进一步求出函数g(x)在[-$\frac{π}{6}$,$\frac{π}{2}$]上的值域.
解答 解:(1)f(x)=$\frac{\sqrt{2}}{2}$sin(2x+$\frac{π}{4}$)+sin2x
=$\frac{\sqrt{2}}{2}(\frac{\sqrt{2}}{2}sin2x+\frac{\sqrt{2}}{2}cos2x)+si{n}^{2}x$
=$\frac{1}{2}$sin2x+$\frac{1}{2}$cos2x+sin2x
=$\frac{1}{2}$sin2x+$co{s}^{2}x-\frac{1}{2}+si{n}^{2}x$
=$\frac{1}{2}$sin2x+1-$\frac{1}{2}$=$\frac{1}{2}$sin2x+$\frac{1}{2}$,
∴f(x)的最小正周期T=$\frac{2π}{2}=π$;
(2)∵函数g(x)对任意x∈R,有g(x)=f(x+$\frac{π}{6}$),
∴g(x)=$\frac{1}{2}$sin2(x+$\frac{π}{6}$)+$\frac{1}{2}$=$\frac{1}{2}$sin(2x+$\frac{π}{3}$)+$\frac{1}{2}$,
当x∈[-$\frac{π}{6}$,$\frac{π}{2}$]时,则2x+$\frac{π}{3}$∈$[0,\frac{4π}{3}]$,
则$-\frac{\sqrt{3}}{2}$≤sin(2x+$\frac{π}{3}$)≤1,即$-\frac{\sqrt{3}}{2}$×$\frac{1}{2}+\frac{1}{2}$≤g(x)$≤\frac{1}{2}+\frac{1}{2}$,解得$\frac{2-\sqrt{3}}{4}$≤g(x)≤1.
综上所述,函数g(x)在[-$\frac{π}{6}$,$\frac{π}{2}$]上的值域为:[$\frac{2-\sqrt{3}}{4}$,1].
点评 本题考查了三角函数的周期性及其求法,考查了函数值域的求法,是中档题.


科目:高中数学 来源: 题型:解答题
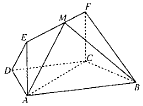 如图,在四边形ABCD中,AB∥CD,∠BCD=$\frac{2π}{3}$,四边形ACFE为矩形,且CF⊥平面ABCD,AD=CD=BC=CF.
如图,在四边形ABCD中,AB∥CD,∠BCD=$\frac{2π}{3}$,四边形ACFE为矩形,且CF⊥平面ABCD,AD=CD=BC=CF.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
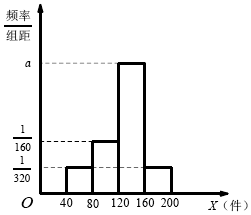 据统计,某物流公司每天的业务中,从甲地到乙地的可配送的货物量X(40≤X<200,单位:件)的频率分布直方图,如图所示,将频率视为概率,回答以下问题.
据统计,某物流公司每天的业务中,从甲地到乙地的可配送的货物量X(40≤X<200,单位:件)的频率分布直方图,如图所示,将频率视为概率,回答以下问题.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
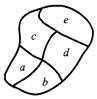 某社区新建了一个休闲小公园,几条小径将公园分成5块区域,如图,社区准备从4种颜色不同的花卉中选择若干种种植在各块区域,要求每个区域随机用一种颜色的花卉,且相邻区域(用公共边的)所选花卉颜色不能相同,则不同种植方法的种数共有( )
某社区新建了一个休闲小公园,几条小径将公园分成5块区域,如图,社区准备从4种颜色不同的花卉中选择若干种种植在各块区域,要求每个区域随机用一种颜色的花卉,且相邻区域(用公共边的)所选花卉颜色不能相同,则不同种植方法的种数共有( )| A. | 96 | B. | 114 | C. | 168 | D. | 240 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com