
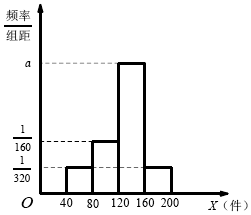
 据统计,某物流公司每天的业务中,从甲地到乙地的可配送的货物量X(40≤X<200,单位:件)的频率分布直方图,如图所示,将频率视为概率,回答以下问题.
据统计,某物流公司每天的业务中,从甲地到乙地的可配送的货物量X(40≤X<200,单位:件)的频率分布直方图,如图所示,将频率视为概率,回答以下问题.分析 (1)计算配送量X在[120,160)上的概率,使用组中值代替各小组的平均值,利用加权平均数公式计算;
(2)设每天的营业利润为Y,对购置车辆数进行依次讨论,分别计算E(Y),根据E(Y)的大小关系作出结论.
解答 解:(1)在区间[120,160)的频率为$1-({\frac{1}{320}+\frac{1}{320}+\frac{1}{160}})×40=\frac{1}{2}$,
该物流公司每天从甲地到乙地平均可配送的货物量:$60×({\frac{1}{320}×40})+100×({\frac{1}{160}×40})+140×\frac{1}{2}+180×({\frac{1}{320}×40})=125$.
(2)从甲地到乙地的可配送货物量X在[40,80),[80,120),[120,160),[160,200)的概率分别为$\frac{1}{8},\frac{1}{4},\frac{1}{2},\frac{1}{8}$.
设运输公司每天的营业利润为Y.
①若购置1辆车,则Y的值为1000;
②若购置2辆车,则Y的可能取值为2000,800,其分而列为
| Y | 2000 | 800 |
| P | $\frac{7}{8}$ | $\frac{1}{8}$ |
| Y | 3000 | 1800 | 600 |
| P | $\frac{5}{8}$ | $\frac{1}{4}$ | $\frac{1}{8}$ |
| Y | 4000 | 2800 | 1600 | 400 |
| P | $\frac{1}{8}$ | $\frac{1}{2}$ | $\frac{1}{4}$ | $\frac{1}{8}$ |
点评 本题考查了频率分布直方图,离散型随机变量的分布列和数学期望,属于中档题.


 优加精卷系列答案
优加精卷系列答案科目:高中数学 来源: 题型:选择题
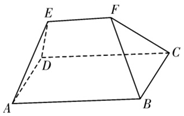 中国古代数学家名著《九章算术》中记载:“刍甍者,下有袤有广,而上有袤无广.刍,草也.甍,屋盖也.”翻译为“底面有长有宽为矩形,顶部只有长没有宽为一条棱.刍甍字面意思为茅草屋顶.”现有一个刍甍如图所示,四边形ABCD为正方形,四边形ABFE、CDEF为两个全等的等腰梯形,AB=4,EF$\underset{∥}{=}$$\frac{1}{2}$AB,若这个刍甍的体积为$\frac{40}{3}$,则异面直线AB与CF所成角的余弦值为( )
中国古代数学家名著《九章算术》中记载:“刍甍者,下有袤有广,而上有袤无广.刍,草也.甍,屋盖也.”翻译为“底面有长有宽为矩形,顶部只有长没有宽为一条棱.刍甍字面意思为茅草屋顶.”现有一个刍甍如图所示,四边形ABCD为正方形,四边形ABFE、CDEF为两个全等的等腰梯形,AB=4,EF$\underset{∥}{=}$$\frac{1}{2}$AB,若这个刍甍的体积为$\frac{40}{3}$,则异面直线AB与CF所成角的余弦值为( )| A. | $\frac{1}{3}$ | B. | $\frac{2}{3}$ | C. | $\frac{\sqrt{5}}{3}$ | D. | $\frac{2\sqrt{2}}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | 1 | C. | 2 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{5}$ | B. | $\frac{2}{5}$ | C. | $\frac{3}{5}$ | D. | $\frac{4}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3}{4}$ | B. | $\frac{3}{8}$ | C. | $\frac{1}{8}$ | D. | $\frac{1}{4}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com