
| A. | $\frac{1}{2}$ | B. | 1 | C. | 2 | D. | 4 |
分析 方法一:根据题意画出图形,根据题意可得△PQF为等边三角形,继而可得F为HR的中点,问题得以解决.
方法二:设P点的坐标为(x0,y0),根据题意求出x0=3,再根据四边形QMRF为平行四边形,即可求出PR=QM=2
解答 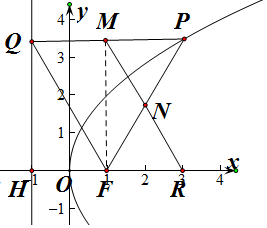 解:方法一:如图所示:连接MF,QF,
解:方法一:如图所示:连接MF,QF,
∵y2=4x的焦点为F,准线为l,P为C上一点
∴FH=2,PF=PQ
∵M,N分别为PQ,PF的中点,
∴MN∥QF,
∵PQ垂直l于点Q,
∴PQ∥OR,
∵PQ=PF,∠NRF=60°,
∴△PQF为等边三角形,
∴MF⊥PQ,
∴F为HR的中点,
∴FR=FH=2,
方法二:设P点的坐标为(x0,y0)
M,N分别为PQ,PF的中点,
∴MN∥QF,
∵∠NRF=60°,
∴∠QFH=60°,
∵∵y2=4x的焦点为F,准线为l,P为C上一点
∴FH=2,PF=PQ
∴QH=HF•tan60°=2$\sqrt{3}$,
∵PQ垂直l于点Q
∴y0=2$\sqrt{3}$,
∴x0=3,
∴PQ=1+3=4,
∴QM=2,
∵四边形QMRF为平行四边形,
∴PR=QM=2
故选:C
点评 本题考查了抛物线的简单性质,以及等边三角形的性质,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{5}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 向左平移$\frac{π}{3}$个单位长度 | B. | 向右平移$\frac{π}{3}$个单位长度 | ||
| C. | 向左平移$\frac{π}{6}$个单位长度 | D. | 向右平移$\frac{π}{6}$个单位长度 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {4,5} | B. | {3,4,5} | C. | {x|3≤x<4} | D. | {x|3≤x≤5} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
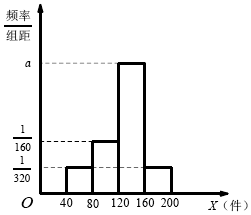 据统计,某物流公司每天的业务中,从甲地到乙地的可配送的货物量X(40≤X<200,单位:件)的频率分布直方图,如图所示,将频率视为概率,回答以下问题.
据统计,某物流公司每天的业务中,从甲地到乙地的可配送的货物量X(40≤X<200,单位:件)的频率分布直方图,如图所示,将频率视为概率,回答以下问题.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{x^2}{3}-{y^2}=1$ | B. | $\frac{y^2}{3}-{x^2}=1$ | C. | ${x^2}-\frac{y^2}{3}=1$ | D. | ${y^2}-\frac{x^2}{3}=1$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $-\frac{1}{2}$ | B. | $\frac{{\sqrt{2}}}{2}$ | C. | $\frac{{\sqrt{3}}}{2}$ | D. | $\frac{1}{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com