
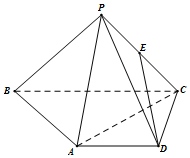
 在四棱锥P-ABCD中,AD∥BC,AD=AB=DC=$\frac{1}{2}$BC=1,E是PC的中点,面PAC⊥面ABCD.
在四棱锥P-ABCD中,AD∥BC,AD=AB=DC=$\frac{1}{2}$BC=1,E是PC的中点,面PAC⊥面ABCD.分析 (Ⅰ)取PB的中点F,连接AF,EF,由三角形的中位线定理可得四边形ADEF是平行四边形.得到DE∥AF,再由线面平行的判定可得ED∥面PAB;
(Ⅱ)法一、取BC的中点M,连接AM,由题意证得A在以BC为直径的圆上,可得AB⊥AC,找出二面角A-PC-D的平面角.求解三角形可得二面角A-PC-D的余弦值.
法二、由题意证得AB⊥AC.又面PAC⊥平面ABCD,可得AB⊥面PAC.以A为原点,$\overrightarrow{AC},\overrightarrow{AB}$方向分别为x轴正方向,y轴正方向建立空间直角坐标系.求出P的坐标,再求出平面PDC的一个法向量,由图可得$\overrightarrow{AB}$为面PAC的一个法向量,由两法向量所成角的余弦值可得二面角A-PC-D的余弦值.
解答 (Ⅰ)证明:取PB的中点F,连接AF,EF.
∵EF是△PBC的中位线,∴EF∥BC,且EF=$\frac{1}{2}BC$.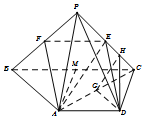
又AD=BC,且AD=$\frac{1}{2}BC$,∴AD∥EF且AD=EF,
则四边形ADEF是平行四边形.
∴DE∥AF,又DE?面ABP,AF?面ABP,
∴ED∥面PAB;
(Ⅱ)解:法一、取BC的中点M,连接AM,则AD∥MC且AD=MC,
∴四边形ADCM是平行四边形,
∴AM=MC=MB,则A在以BC为直径的圆上.
∴AB⊥AC,可得$AC=\sqrt{3}$.
过D作DG⊥AC于G,
∵平面PAC⊥平面ABCD,且平面PAC∩平面ABCD=AC,
∴DG⊥平面PAC,则DG⊥PC.
过G作GH⊥PC于H,则PC⊥面GHD,连接DH,则PC⊥DH,
∴∠GHD是二面角A-PC-D的平面角.
在△ADC中,$GD=\frac{1}{2}$,连接AE,$GH=\frac{1}{2}AE=\frac{{\sqrt{2}}}{2}$.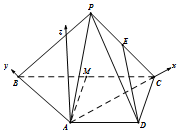
在Rt△GDH中,$HD=\frac{{\sqrt{3}}}{2}$,
∴$cos∠GHD=\frac{GH}{HD}=\frac{{\sqrt{6}}}{3}$,
即二面角A-PC-D的余弦值$\frac{{\sqrt{6}}}{3}$.
法二、取BC的中点M,连接AM,则AD∥MC,且AD=MC.
∴四边形ADCM是平行四边形,
∴AM=MC=MB,则A在以BC为直径的圆上,
∴AB⊥AC.
∵面PAC⊥平面ABCD,且平面PAC∩平面ABCD=AC,∴AB⊥面PAC.
如图以A为原点,$\overrightarrow{AC},\overrightarrow{AB}$方向分别为x轴正方向,y轴正方向建立空间直角坐标系.
可得$C({\sqrt{3},0,0})$,$D({\frac{{\sqrt{3}}}{2},-\frac{1}{2},0})$.
设P(x,0,z),(z>0),依题意有$|{PA}|=\sqrt{{x^2}+{z^2}}=\sqrt{3}$,$|{PC}|=\sqrt{{{({x-\sqrt{3}})}^2}+{z^2}}=2$,
解得$x=\frac{{\sqrt{3}}}{3},z=\frac{{2\sqrt{6}}}{3}$.
则$P({\frac{{\sqrt{3}}}{3},0,\frac{{2\sqrt{6}}}{3}})$,$\overrightarrow{DC}=({\frac{{\sqrt{3}}}{2},\frac{1}{2},0})$,$\overrightarrow{CP}=({-\frac{{2\sqrt{3}}}{3},0,\frac{{2\sqrt{6}}}{3}})$.
设面PDC的一个法向量为$\overrightarrow{n}=({x}_{0},{y}_{0},{z}_{0})$,
由$\left\{\begin{array}{l}{\overrightarrow{n}•\overrightarrow{DC}=\frac{\sqrt{3}}{2}{x}_{0}+\frac{1}{2}{y}_{0}=0}\\{\overrightarrow{n}•\overrightarrow{CP}=-\frac{2\sqrt{3}}{3}{x}_{0}+\frac{2\sqrt{6}}{3}{z}_{0}=0}\end{array}\right.$,取x0=1,得$\overrightarrow n=({1,-\sqrt{3},\frac{{\sqrt{2}}}{2}})$.
$\overrightarrow{AB}$为面PAC的一个法向量,且$\overrightarrow{AB}=({0,1,0})$,
设二面角A-PC-D的大小为θ,
则有$cosθ=|{\frac{{\overrightarrow{AB}•\overrightarrow n}}{{|{\overrightarrow{AB}}||{\overrightarrow n}|}}}|=\frac{{\sqrt{6}}}{3}$,即二面角A-PC-D的余弦值$\frac{{\sqrt{6}}}{3}$.
点评 本题考查直线与平面平行的判定,考查空间想象能力和思维能力,训练了利用空间向量求二面角的平面角,是中档题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 36π | B. | 64π | C. | 100π | D. | 104π |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1-i | B. | 1+i | C. | -1-i | D. | -1+i |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
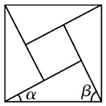 《周髀算经》中给出了弦图,所谓弦图是由四个全等的直角三角形和中间一个小正方形拼成一个大的正方形,若图中直角三角形两锐角分别为α、β,且小正方形与大正方形面积之比为4:9,则cos(α-β)的值为( )
《周髀算经》中给出了弦图,所谓弦图是由四个全等的直角三角形和中间一个小正方形拼成一个大的正方形,若图中直角三角形两锐角分别为α、β,且小正方形与大正方形面积之比为4:9,则cos(α-β)的值为( )| A. | $\frac{5}{9}$ | B. | $\frac{4}{9}$ | C. | $\frac{2}{3}$ | D. | 0 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com