
分析 运用两渐近线的对称性和条件,可得A为BF的中点,由垂直平分线的性质和等腰三角形的性质,可得Rt△OAB中,∠AOB=$\frac{π}{3}$,求得渐近线的斜率,运用离心率公式即可得到.
解答 解:当b>a>0时,由$\frac{{|{AF}|}}{{|{BF}|}}=\frac{1}{2}$,可知A为BF的中点,
由∠AOF=∠AOB=∠BOF'=60°,可得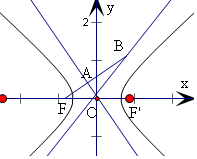 $\frac{|OA|}{|OB|}$=$\frac{1}{2}$,
$\frac{|OA|}{|OB|}$=$\frac{1}{2}$,
则Rt△OAB中,∠AOB=$\frac{π}{3}$,
渐近线OB的斜率k=$\sqrt{3}$,
即离心率e=$\frac{c}{a}$=$\sqrt{1+3}$=2.
同理当a>b>0时,可得e=$\frac{2}{3}\sqrt{3}$;
故答案为:$\frac{2}{3}\sqrt{3}$或2.
点评 本题考查双曲线的性质和应用,主要是离心率的求法,考查分类讨论的数学思想,属于中档题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
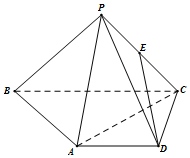 在四棱锥P-ABCD中,AD∥BC,AD=AB=DC=$\frac{1}{2}$BC=1,E是PC的中点,面PAC⊥面ABCD.
在四棱锥P-ABCD中,AD∥BC,AD=AB=DC=$\frac{1}{2}$BC=1,E是PC的中点,面PAC⊥面ABCD.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ∅ | B. | {(3,0),(0,2)} | C. | [一2,2] | D. | [一3,3] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
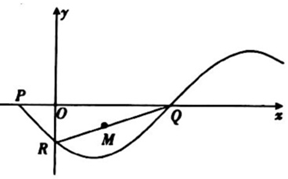 如图,函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<π)的部分图象与坐标轴的三个交点分别为P(-1,0),Q、R,且线段RQ的中点M的坐标为($\frac{3}{2}$,-$\frac{1}{2}$),则f(-2)等于( )
如图,函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<π)的部分图象与坐标轴的三个交点分别为P(-1,0),Q、R,且线段RQ的中点M的坐标为($\frac{3}{2}$,-$\frac{1}{2}$),则f(-2)等于( )| A. | 1 | B. | -1 | C. | $\frac{\sqrt{6}}{2}$ | D. | -$\frac{\sqrt{6}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2倍以上,但不超过3倍 | B. | 3倍以上,但不超过4倍 | ||
| C. | 4倍以上,但不超过5倍 | D. | 5倍以上,但不超过6倍 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
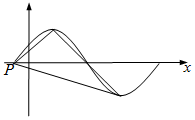 已知函数$f(x)=sin2x+sin(\frac{π}{3}-2x)$.
已知函数$f(x)=sin2x+sin(\frac{π}{3}-2x)$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com