
(2010•上海模拟)在10件产品中有2件次品,任意抽取3件,则抽到次品个数的数学期望的值是 .
科目:高中数学 来源:2014-2015学年上海市高二上学期第一次月考数学试卷(解析版) 题型:解答题
已知正项数列 ,
, ,且
,且
(1)求证: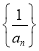 是等差数列,并求
是等差数列,并求 的通项公式;
的通项公式;
(2)数列 满足
满足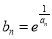 ,若
,若 ,仍是
,仍是 中的项,求
中的项,求 在区间
在区间 中的所有可能值之和
中的所有可能值之和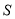 ;
;
(3)若将上述递推关系 改为:
改为: ,且数列
,且数列 中任意项
中任意项 ,试求满足要求的实数
,试求满足要求的实数 的取值范围
的取值范围
查看答案和解析>>
科目:高中数学 来源:[同步]2014年北师大版选修4-1 2.2直线与球、平面与球位置关系(解析版) 题型:填空题
已知球O的半径为4,圆M与圆N为该球的两个小圆,AB为圆M与圆N的公共弦,AB=4,若OM=ON=3,则两圆圆心的距离MN= .
查看答案和解析>>
科目:高中数学 来源:[同步]2014年北师大版选修2-3 2.2超几何分布练习卷(解析版) 题型:解答题
如图,曲线Γ:x2+y2=1(x≥0,y≥0)与x轴交于点A,点P在曲线Γ上,∠AOP=α.
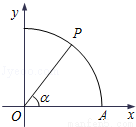
(Ⅰ)若点P的坐标是(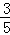 ,
, ),求cos2
),求cos2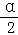 ﹣sin2
﹣sin2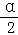 +2sin
+2sin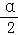 cos
cos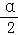 的值;
的值;
(Ⅱ)求函数f(α)=sinα+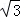 cosα的值域.
cosα的值域.
查看答案和解析>>
科目:高中数学 来源:[同步]2014年北师大版选修2-3 2.2超几何分布练习卷(解析版) 题型:解答题
(2009•朝阳区二模)在袋子中装有10个大小相同的小球,其中黑球有3个,白球有n(2≤n≤5,且n≠3)个,其余的球为红球.
(Ⅰ)若n=5,从袋中任取1个球,记下颜色后放回,连续取三次,求三次取出的球中恰有2个红球的概率;
(Ⅱ)从袋里任意取出2个球,如果这两个球的颜色相同的概率是 ,求红球的个数;
,求红球的个数;
(Ⅲ)在(Ⅱ)的条件下,从袋里任意取出2个球.若取出1个白球记1分,取出1个黑球记2分,取出1个红球记3分.用ξ表示取出的2个球所得分数的和,写出ξ的分布列,并求ξ的数学期望Eξ.
查看答案和解析>>
科目:高中数学 来源:[同步]2014年北师大版选修2-2 2.5简单复合函数求导法则练习卷(解析版) 题型:?????
设f(x)=sinxcosx,那么f′(x)=( )
A.﹣cosxsinx B.cos2x C.sinx+cosx D.cosx﹣sinx
查看答案和解析>>
科目:高中数学 来源:[同步]2014年北师大版选修2-2 2.5简单复合函数求导法则练习卷(解析版) 题型:?????
已知函数f(x)=cos(x+ϕ)(0<ϕ<π)的导函数f'(x)的图象如图所示,则ϕ=( )
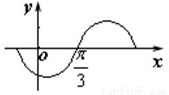
A.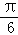 B.
B.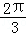 C.
C.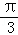 D.
D.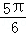
查看答案和解析>>
科目:高中数学 来源:[同步]2014年北师大版选修2-2 2.4导数的四则运算法则练习卷(解析版) 题型:?????
已知函数f(x)=x+lnx,则f′(1)的值为( )
A.1 B.2 C.﹣1 D.﹣2
查看答案和解析>>
科目:高中数学 来源:[同步]2014年北师大版选修2-1 2.1从平面向量到空间向量练习卷(解析版) 题型:选择题
如图,棱长为2的正方体ABCD﹣A1B1C1D1在空间直角坐标系中,若E,F分别是BC,DD1中点,则 的坐标为( )
的坐标为( )
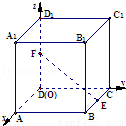
A.(1,2,﹣1) B.(﹣1,2,﹣1) C.(1,﹣2,﹣1) D.(﹣1,﹣2,1)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com