
(本小题10分)选修4—4:坐标系与参数方程设椭圆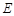 的普通方程为
的普通方程为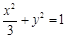
(1)设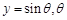 为参数,求椭圆
为参数,求椭圆 的参数方程;
的参数方程;
(2)点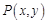 是椭圆
是椭圆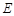 上的动点,求
上的动点,求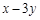 的取值范围.
的取值范围.
 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案 双基同步导航训练系列答案
双基同步导航训练系列答案 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案科目:高中数学 来源: 题型:解答题
(12分)在平面直角坐标系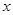 O
O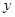 中,直线
中,直线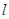 与抛物线
与抛物线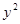 =2
=2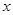 相交于A、B两点.
相交于A、B两点.
(Ⅰ)求证:命题“如果直线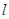 过点T(3,0),那么
过点T(3,0),那么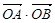 =3”是真命题;
=3”是真命题;
(Ⅱ)写出(1)中命题的逆命题,判断它是真命题还是假命题,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
在平面直角坐标系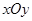 中,椭圆
中,椭圆 为
为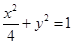
(1)若一直线与椭圆 交于两不同点
交于两不同点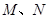 ,且线段
,且线段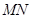 恰以点
恰以点 为中点,求直线
为中点,求直线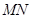 的方程;
的方程;
(2)若过点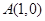 的直线
的直线 (非
(非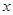 轴)与椭圆
轴)与椭圆 相交于两个不同点
相交于两个不同点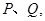 试问在
试问在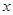 轴上是否存在定点
轴上是否存在定点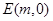 ,使
,使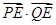 恒为定值
恒为定值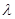 ?若存在,求出点
?若存在,求出点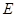 的坐标及实数
的坐标及实数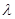 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
直线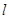 与椭圆
与椭圆 交于
交于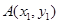 ,
,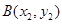 两点,已知
两点,已知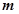
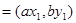 ,
,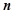
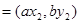 ,若
,若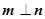 且椭圆的离心率
且椭圆的离心率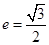 ,又椭圆经过点
,又椭圆经过点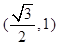 ,
,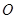 为坐标原点.
为坐标原点.
(Ⅰ)求椭圆的方程;
(Ⅱ)若直线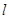 过椭圆的焦点
过椭圆的焦点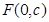 (
(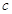 为半焦距),求直线
为半焦距),求直线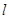 的斜率
的斜率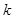 的值;
的值;
(Ⅲ)试问: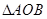 的面积是否为定值?如果是,请给予证明;如果不是,请说明理由.
的面积是否为定值?如果是,请给予证明;如果不是,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某公园内有一椭圆形景观水池,经测量知,椭圆长轴长为20米,短轴长为16米,现以椭圆长轴所在直线为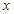 轴,短轴所在直线为
轴,短轴所在直线为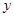 轴,建立平面直角坐标系,如图所示:
轴,建立平面直角坐标系,如图所示: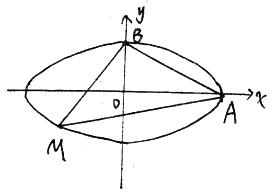
(1)为增加景观效果,拟在水池内选定两点安装水雾喷射口,要求椭圆上各点到这两点距离之和都相等,请指出水雾喷射口的位置(用坐标表示),并求椭圆的方程。
(2)为了增加水池的观赏性,拟划出一个以椭圆的长轴顶点A、短轴顶点B及椭圆上某点M构成的三角形区域进行夜景灯光布置,请确定点M的位置,使此三角形区域面积最大。
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知抛物线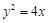 ,点
,点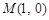 关于
关于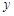 轴的对称点为
轴的对称点为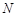 ,直线
,直线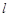 过点
过点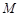 交抛物线于
交抛物线于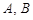 两点.
两点.
(1)证明:直线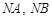 的斜率互为相反数;
的斜率互为相反数;
(2)求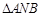 面积的最小值;
面积的最小值;
(3)当点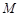 的坐标为
的坐标为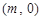 ,
,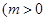 且
且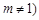 .根据(1)(2)推测并回答下列问题(不必说明理由):①直线
.根据(1)(2)推测并回答下列问题(不必说明理由):①直线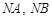 的斜率是否互为相反数? ②
的斜率是否互为相反数? ②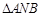 面积的最小值是多少?
面积的最小值是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图,曲线C1是以原点O为中心,F1、F2为焦点的椭圆的一部分,曲线C2是以原点O为顶点,F2为焦点的抛物线的一部分,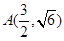 是曲线C1和C2的交点.
是曲线C1和C2的交点.
(Ⅰ)求曲线C1和C2所在的椭圆和抛物线的方程;
(Ⅱ)过F2作一条与x轴不垂直的直线,分别与曲线C1、C2依次交于B、C、D、E四点,若G为CD中点,H为BE中点,问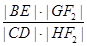 是否为定值,若是,求出定值;若不是,请说明理由.
是否为定值,若是,求出定值;若不是,请说明理由.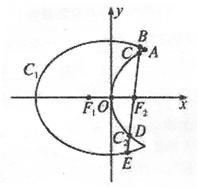
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图,曲线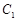 是以原点O为中心、
是以原点O为中心、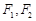 为焦点的椭圆的一部分,曲线
为焦点的椭圆的一部分,曲线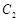 是以O为顶点、
是以O为顶点、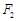 为焦点的抛物线的一部分,A是曲线
为焦点的抛物线的一部分,A是曲线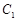 和
和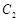 的交点
的交点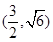 且
且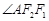 为钝角.
为钝角. 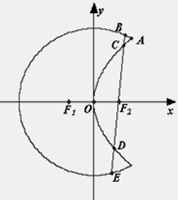
(1)求曲线 和
和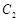 的方程;
的方程;
(2)过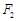 作一条与
作一条与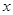 轴不垂直的直线,分别与曲线
轴不垂直的直线,分别与曲线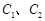 依次交于B、C、D、E四点,若G为CD中点、H为BE中点,问
依次交于B、C、D、E四点,若G为CD中点、H为BE中点,问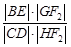 是否为定值?若是求出定值;若不是说明理由.
是否为定值?若是求出定值;若不是说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com