
| A. | 0 | B. | -2012 | C. | -2013 | D. | -2014 |
分析 根据对数函数的单调性得出各项的值,在进行计算.
解答 解:由对数函数的单调性可知[lg1]=[lg2]=…=[lg9]=0,
[lg10]=[lg11]=[lg12]=…=[lg99]=1,
[lg100]=[lg101]=…=[lg999]=2,
[lg1000]=[lg1001]=…=[lg2016]=3.
[lg$\frac{1}{2}$]=[lg$\frac{1}{3}$]=…=[lg$\frac{1}{10}$]=-1,
[lg$\frac{1}{11}$]=[lg$\frac{1}{12}$]=…=[lg$\frac{1}{100}$]=-2,
[lg$\frac{1}{101}$]=[lg$\frac{1}{102}$]=…=[lg$\frac{1}{1000}$]=-3,
[lg$\frac{1}{1001}$]=[lg$\frac{1}{1002}$]=…=[lg$\frac{1}{2016}$]=-4.
∴S=0×9+1×90+2×900+3×1017+(-1)×9+(-2)×90+(-3)×900+(-4)×1016=-2012.
故选:B.
点评 本题考查了对数的运算性质,对数函数的单调性,属于中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 3 | C. | 6 | D. | 7 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $[\frac{2}{3},\frac{4}{3}]$ | B. | $[\frac{1}{3},\frac{2}{3}]$ | C. | [0,2] | D. | $[0,\frac{{2\sqrt{5}}}{3}]$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
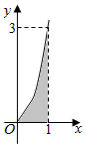 已知函数f(x)的部分图象如图所示,向图中的矩形区域随机投出100粒豆子,记下落入阴影区域的豆子数.通过10次这样的试验,算得落入阴影区域的豆子的平均数约为39,由此可估计$\int\begin{array}{l}1\\ 0\end{array}f(x)dx$的值约为( )
已知函数f(x)的部分图象如图所示,向图中的矩形区域随机投出100粒豆子,记下落入阴影区域的豆子数.通过10次这样的试验,算得落入阴影区域的豆子的平均数约为39,由此可估计$\int\begin{array}{l}1\\ 0\end{array}f(x)dx$的值约为( )| A. | $\frac{61}{100}$ | B. | $\frac{39}{100}$ | C. | $\frac{10}{100}$ | D. | $\frac{117}{100}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com