(本小题满分12分)已知全集为实数集R,集合
，
．
（Ⅰ）分别求
，
；
（Ⅱ）已知集合
，若
，求实数
的取值集合．
(Ⅰ)
,
=
;(Ⅱ)
.
解析试题分析： （I）集合A是函数的定义域，集合B是不等式
的解集，然后得到集合A，B再利用集合的交并补运算的定义求解即可.
（II）因为，所以
和
，然后分两种情况进行研究即可.
(Ⅰ)
…………………………………………………………………2分
…………………………………………………4分……………………………………………………………5分
……………………………6分
(Ⅱ) ①当
时，
，此时；…………………………………………9分
②当
时，，则
……………………………………………11分
综合①②，可得的取值范围是 ………………………………………12分
考点：集合的运算，求函数的定义域，解对数不等式.
点评：研究集合时，一定要注意代表元素是谁，然后再求出代表元素的取值范围，即可确定其集合.再进行运算时要把交，并，补的运算定义记清楚，另外遇到，要注意按和两种情况考虑.
小学课时作业全通练案系列答案
金版课堂课时训练系列答案
单元全能练考卷系列答案科目：高中数学 来源： 题型：解答题
（本题满分15分）已知集合M={1，2，3，4，5}，
.
（1）用列举法表示集合
；
(2)设N是M的非空真子集，且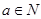
时，有
，试写出所有集合N；
(3)已知M的非空子集个数为31个，依次记为
，分别求出它们各自的元素之和，结果依次记为
，试计算：
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
}，B={
}，求集合
，
；
，
, 求非零实数
的值。
，集合
，
，
、
；
是集合
的子集，求实数
的取值范围. 
且
，求实数
的取值范围．
，求
的值
，
.
；
的解集是
，求实数
，
的值
,集合
;
,求
的取值范围.
,函数合
,函
的定义域为集数
的定义域为集合
.