
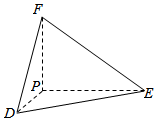
 (1)类比平面内直角三角形ABC的勾股定理,试给出空间中四面体P-DEF性质的猜想;
(1)类比平面内直角三角形ABC的勾股定理,试给出空间中四面体P-DEF性质的猜想;分析 (1)类比平面内直角三角形ABC的勾股定理,即可给出空间中四面体P-DEF性质;
(2)设三个侧棱是a,b,c,可得三个侧面的面积,底面△DEF的面积,从而可得结论.
解答 (1)解:底面△DEF的面积为S0,三个侧面的面积分别为S1,S2,S3,则S02=S12+S22+S32.
(2)证明:设三个侧棱是a,b,c,则三个侧面的面积分别是$\frac{ab}{2}$,$\frac{bc}{2}$,$\frac{ac}{2}$.
三条底边的长为$\sqrt{{a}^{2}+{b}^{2}}$,$\sqrt{{b}^{2}+{c}^{\;}}$,$\sqrt{{a}^{2}+{c}^{2}}$,
由余弦定理,可得底面的面积是$\frac{\sqrt{(ab)^{2}+(ac)^{2}+(bc)^{2}}}{2}$
∵底面△DEF的面积为S0,三个侧面的面积分别为S1,S2,S3,
∴S02=S12+S22+S32.
点评 本题考查类比推理,考查学生分析解决问题的能力,考查学生的计算能力,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | $\frac{8}{15}$ | B. | $\frac{4}{15}$ | C. | $\frac{2}{15}$ | D. | $\frac{1}{15}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | p2+q2+r2+pq+qr+rp=d2 | B. | p3+q3+r3=d3 | ||
| C. | p2+q2+r2=d2 | D. | p+q+r=d |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ①② | B. | ②③ | C. | ①④ | D. | ②④ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [$\frac{1}{3}$ln2,+∞) | B. | [0,$\frac{1}{3}$ln2] | C. | (-∞,0] | D. | (-∞,$\frac{1}{3}$ln2] |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com