Question

19．若函数f（x）=ax³-3x²+1存在唯一的零点x₀，且x₀＜0，则实数a的取值范围是（2，+∞）．

Answer 1

分析 （i）当a=0时，f（x）=-3x²+1，令f（x）=0，解得x=$±\frac{\sqrt{3}}{3}$，舍去．
（ii）当a≠0时，f′（x）=3ax²-6x=3ax（x-$\frac{2}{a}$），令f′（x）=0，解得x=0或$\frac{2}{a}$．对a分类讨论：①当a＜0时，由题意可得：$\left\{\begin{array}{l}{\frac{2}{a}＜0}\\{f（x）_{min}＜0}\end{array}\right.$；②当a＞0时，由题意可得f（x）_min=$f（\frac{2}{a}）$＞0，解出判定即可．

解答 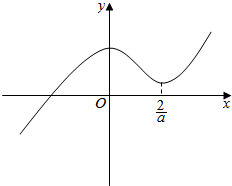解：（i）当a=0时，f（x）=-3x²+1，令f（x）=0，解得x=$±\frac{\sqrt{3}}{3}$，函数f（x）有两个零点，舍去．
（ii）当a≠0时，f′（x）=3ax²-6x=3ax（x-$\frac{2}{a}$），令f′（x）=0，解得x=0或$\frac{2}{a}$．
①当a＜0时，$\frac{2}{a}$＜0，当$x＜\frac{2}{a}$或x＞0时，f′（x）＜0，此时函数f（x）单调递减；当$\frac{2}{a}＜x＜0$时，f′（x）＞0，此时函数f（x）单调递增．
∴$\frac{2}{a}$是函数f（x）的极小值点，0是函数f（x）的极大值点．
∵函数f（x）=ax³-3x²+1存在唯一的零点x₀，且x₀＜0，则$\left\{\begin{array}{l}{\frac{2}{a}＜0}\\{f（0）＜0}\end{array}\right.$，无解，舍去．
②当a＞0时，$\frac{2}{a}$＞0，当x＞$\frac{2}{a}$或x＜0时，f′（x）＞0，此时函数f（x）单调递增；当$0＜x＜\frac{2}{a}$时，f′（x）＜0，此时函数f（x）单调递减．
∴$\frac{2}{a}$是函数f（x）的极小值点，0是函数f（x）的极大值点．
∵函数f（x）=ax³-3x²+1存在唯一的零点x₀，且x₀＜0，则$f（\frac{2}{a}）$＞0，即$\frac{8}{{a}^{2}}$-$\frac{12}{{a}^{2}}$+1＞0，a＞0，解得a＞2．
综上可得：实数a的取值范围是（2，+∞）．
故答案为：（2，+∞）．

点评 本题考查了利用导数研究函数的单调性极值与最值、函数的零点，考查了分类讨论方法、推理能力与计算能力，属于中档题．