练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    20．已知A，B，C是球O的球面上三点，若三棱锥O-ABC体积的最大值为1，则球O的体积为8π．

    分析 当点C位于垂直于面AOB的直径端点且∠AOB=90°时，三棱锥O-ABC的体积最大，利用三棱锥O-ABC体积的最大值为1，求出半径，即可求出球O的体积．

    解答 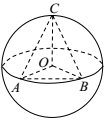解：如图所示，当点C位于垂直于面AOB的直径端点且∠AOB=90°时，三棱锥O-ABC的体积最大，设球O的半径为R，此时VO-ABC=VC-AOB=$\frac{1}{3}×\frac{1}{2}×R×R×R$=1，
    ∴R3=6，则球O的体积为$\frac{4}{3}π{R}^{3}$=8π．
    故答案为8π．

    点评 本题考查球的半径，考查体积的计算，确定点C位于垂直于面AOB的直径端点时，三棱锥O-ABC的体积最大是关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    10．设l，m表示不同直线，α，β表示不同平面，则下列结论中正确的是（　　）
    A．若l∥α，l⊥m，则m⊥αB．若l∥α，l⊥m，m?β，则α⊥β
    C．若l∥α，l∥m，则m∥αD．若α∥β，l∥α，l∥m，m?β，则m∥β

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    11．已知集合A={1，2，3}，B={1，3}，则A∩B=（　　）
    A．{2}B．{1，3}C．{1，2}D．{1，2，3}

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    8．已知直线l：$\left\{\begin{array}{l}x=1+\frac{1}{2}t\\ y=\frac{{\sqrt{3}}}{2}t\end{array}\right.$（t为参数），曲线C1：$\left\{\begin{array}{l}x=cosθ\\ y=sinθ\end{array}\right.$（θ为参数）．
    （1）设l与C1相交于A，B两点，求|AB|；
    （2）若把曲线C1上各点的横坐标伸长为原来的$\sqrt{3}$倍，纵坐标伸长为原来的3倍，得到曲线C2，设点P是曲线C2上的一个动点，求它到直线l的距离的最大值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    15．设x，y满足约束条件$\left\{\begin{array}{l}{2x+y-6≤0}\\{x-y-1≤0}\\{x-1≥0}\end{array}\right.$，若z=ax+2y仅在点（$\frac{7}{3}$，$\frac{4}{3}$）处取得最大值，则a的值可以为（　　）
    A．-8B．-4C．4D．8

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

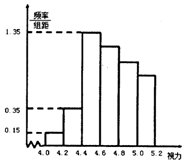    5．某校高一共录取新生1000名，为了解学生视力情况，校医随机抽取了100名学生进行视力测试，并得到如下频率分布直方图．
    （Ⅰ）若视力在4.6～4.8的学生有24人，试估计高一新生视力在4.8以上的人数；
    1～50名951～1000名
    近视4132
    不近视918
    （Ⅱ）校医发现学习成绩较高的学生近视率较高，又在抽取的100名学生中，对成绩在前50名的学生和其他学生分别进行统计，得到如右数据，根据这些数据，校医能否有超过95%的把握认为近视与学习成绩有关？
    （Ⅲ）用分层抽样的方法从（Ⅱ）中27名不近视的学生中抽出6人，再从这6人中任抽2人，其中抽到成绩在前50名的学生人数为ξ，求ξ的分布列和数学期望．
    附：K2=$\frac{n（ad-bc）^{2}}{（a+b）（c+d）（a+c）（b+d）}$
    P（K2≥k）0.100.050.0250.0100.005
    k2.7063.8415.0246.6357.879

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    12．已知函数f（x）=$\left\{\begin{array}{l}{{2}^{x}，x＜0}\\{m-{x}^{2}，x≥0}\end{array}\right.$，给出下列两个命题：命题p：?m∈（-∞，0），方程f（x）=0有实数解；命题q：当m=$\frac{1}{4}$时，f（f（-1））=0，则下列命题为真命题的是（　　）
    A．p∧qB．（￢p）∧qC．p∧（￢q）D．（￢p）∧（￢q）

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    9．实数x，y满足$\left\{\begin{array}{l}{x≤4}\\{x+y-2≥0}\\{x-y+8≥0}\end{array}\right.$，若z=$\frac{1}{2}$ax+y的最大值为2a+12，最小值为2a-2，则a的取值范围是[-2，2]．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    10．若实数x，y满足约束条件$\left\{\begin{array}{l}{2x+y≤4}\\{x-y≥1}\\{x-2y≤2}\end{array}\right.$，则目标函数z=3x+y的最大值为（　　）
    A．6B．$\frac{17}{3}$C．$\frac{20}{3}$D．-1

    查看答案和解析>>

    同步练习册答案