
| A. | $\frac{sinx}{x}≥\frac{sina}{a}$ | B. | cosa≥$\frac{sinx}{x}$ | C. | $\frac{3π}{2}$≤a≤2π | D. | a-cosa≥x-cosx |
分析 利用导数研究单调性,运用零点的存在性定理判断出a所在的范围,根据f(x)的正负确定g(x)=$\frac{sinx}{x}$的最小值.
解答 解:f′(x)=xsinx,
当x∈(0,π),f′(x)>0,函数f(x)单调递增,
当x∈(π,2π),f′(x)<0,函数f(x)单调递减,
又f(0)=0,f(π)>0,f(2π)<0,
∴a∈(π,2π),
∴当x∈(0,a),f(x)>0,当x∈(a,2π),f(x)<0,
令g(x)=$\frac{sinx}{x}$,g′(x)=$\frac{xcosx-sinx}{{x}^{2}}$,
∴当x∈(0,a),g′(x)<0,函数g(x)单调递减,当x∈(a,2π),g′(x)>0,函数g(x)单调递增,
∴g(x)≥g(a).
故选:A.
点评 本题主要考查零点的存在性定理,利用导数求最值及计算能力.


科目:高中数学 来源: 题型:选择题
 已知正方体ABCD-A1B1C1D1的棱长为2,点E,F,G,H,I,J分别是该正方体的棱AA1,AB,AD,C1D1,C1B1,C1C的中点,现从该正方体中截去棱锥A-EFG与棱锥C1-HIJ,若正(主)视方向如图所示,则剩余部分的几何体的侧(左)视图为( )
已知正方体ABCD-A1B1C1D1的棱长为2,点E,F,G,H,I,J分别是该正方体的棱AA1,AB,AD,C1D1,C1B1,C1C的中点,现从该正方体中截去棱锥A-EFG与棱锥C1-HIJ,若正(主)视方向如图所示,则剩余部分的几何体的侧(左)视图为( )| A. |  | B. |  | C. |  | D. |  |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{{e}^{2π}(1-{e}^{2015π})}{1-{e}^{2π}}$ | B. | -$\frac{{e}^{2π}(1-{e}^{2015π)}}{1-{e}^{π}}$ | ||
| C. | -$\frac{1-{e}^{2016π}}{1-{e}^{2π}}$ | D. | -$\frac{{e}^{2π}(1-{e}^{2014π})}{1-{e}^{2π}}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
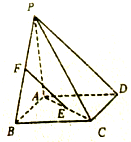 如图四棱锥P-ABCD的底面ABCD是菱形,PA⊥底面ABCD,E,F分别是AC,PB的中点,PA=AB=2,∠BAD=120°.
如图四棱锥P-ABCD的底面ABCD是菱形,PA⊥底面ABCD,E,F分别是AC,PB的中点,PA=AB=2,∠BAD=120°.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | c<b<a | B. | c<a<b | C. | b<a,c | D. | a<b<c |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,已知椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{\sqrt{3}}{2}$,且过点($\sqrt{3}$,$\frac{1}{2}$).
如图,已知椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{\sqrt{3}}{2}$,且过点($\sqrt{3}$,$\frac{1}{2}$).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com