
分析 (1)若m=n=k=1,求导数,利用导数的正负,求f(x)的单调区间;
(2)若n=k=1,且当x≥0时,f(x)≥1总成立,先确定m≥0,在分类讨论,确定函数的最小值,即可求实数m的取值范围;
(3)令f′(x)=0,x1+x2=2,x1x2=$\frac{1}{m}$,再结合基本不等式,即可证明结论.
解答 (1)解:m=n=k=1,f′(x)=$\frac{{e}^{x}({x}^{2}-x)}{({x}^{2}+x+1)^{2}}$,
∴0<x<1,f′(x)<0,x<0或x>1时,f′(x)>0,
∴函数的单调减区间是(0,1),单调增区间是(-∞,0),(1,+∞);
(2)解:若n=k=1,且当x≥0时,f(x)≥1总成立,则m≥0.
m=0,f(x)=$\frac{{e}^{x}}{x+1}$,f′(x)=$\frac{x{e}^{x}}{(x+1)^{2}}$≥0,∴f(x)min=f(0)=1;
m>0,f′(x)=$\frac{{e}^{x}•mx•(x+\frac{1-2m}{m})}{(m{x}^{2}+x+1)^{2}}$,
0<m≤$\frac{1}{2}$,f(x)min=f(0)=1;
m≥$\frac{1}{2}$,f(x)在[0,$\frac{2m-1}{m}$]上为减函数,在[$\frac{2m-1}{m}$,+∞)上为增函数,f(x)min<f(0)=1不成立.
综上所述,0≤m≤$\frac{1}{2}$;
(3)证明:f(x)=$\frac{{e}^{x}}{m{x}^{2}+1}$,f′(x)=$\frac{{e}^{x}(m{x}^{2}-2mx+1)}{(m{x}^{2}+1)^{2}}$.
∵f(x)存在两个极值点x1,x2,∴4m2-4m>0,∴m>1.
令f′(x)=0,x1+x2=2,x1x2=$\frac{1}{m}$,
注意到$m{{x}_{i}}^{2}-2m{x}_{i}+1=0$(i=1,2),
∴f(x1)=$\frac{{e}^{{x}_{1}}}{m{{x}_{1}}^{2}+1}=\frac{{e}^{{x}_{1}}}{2m{x}_{1}}$,f(x2)=$\frac{{e}^{{x}_{2}}}{2m{x}_{2}}$,
∴f(x1)+f(x2)=$\frac{{e}^{{x}_{1}}}{2m{x}_{1}}+\frac{{e}^{{x}_{2}}}{2m{x}_{2}}$=$\frac{1}{2}$(${x}_{2}•{e}^{{x}_{1}}+{x}_{1}•{e}^{{x}_{2}}$)
>$\frac{1}{2}•2\sqrt{{x}_{1}{x}_{2}•{e}^{{x}_{1}+{x}_{2}}}$=$e\sqrt{\frac{1}{m}}$=$\frac{e\sqrt{m}}{m}$;
∵$\frac{1}{2}$(${x}_{2}•{e}^{{x}_{1}}+{x}_{1}•{e}^{{x}_{2}}$)<$\frac{({x}_{1}+{x}_{2})({e}^{{x}_{1}}+{e}^{{x}_{2}})}{4}$<$\frac{{e}^{2}+1}{2}$,
∴$\frac{e\sqrt{m}}{m}$<f(x1)+f(x2)<$\frac{{e}^{2}+1}{2}$.
点评 本题考查导数知识的综合运用,考查函数的单调性、最值,考查不等式的证明,考查学生分析解决问题的能力,属于压轴题.


科目:高中数学 来源: 题型:解答题
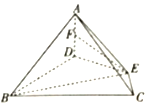 如图,在四棱锥A-BCED中,AD⊥底面BCED,BD⊥DE,∠DBC=∠BCE═60°,BD=2CE.
如图,在四棱锥A-BCED中,AD⊥底面BCED,BD⊥DE,∠DBC=∠BCE═60°,BD=2CE.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 命题“?x0∈R,x02-x0≤0”的否定为“?x∈R,x2-x>0” | |
| B. | 命题“在△ABC中,A>30°,则sinA>$\frac{1}{2}$”的逆否命题为真命题 | |
| C. | 设{an}是公比为q的等比数列,则“q>1”是“{an}为递增数列”的充分必要条件 | |
| D. | 若非零向量$\overrightarrow a$、$\overrightarrow b$满足$|{\overrightarrow a+\overrightarrow b}|=|{\overrightarrow a}|+|{\overrightarrow b}$|,则$\overrightarrow a$与$\overrightarrow b$共线 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{4}{5}$ | B. | $\frac{4}{5}$ | C. | -$\frac{4}{5}$i | D. | $\frac{4}{5}$i |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
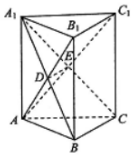 如图,在直三棱柱ABC-A1B1C1中,AC⊥BC,A1B与AB1交于点D,A1C与AC1交于点E.
如图,在直三棱柱ABC-A1B1C1中,AC⊥BC,A1B与AB1交于点D,A1C与AC1交于点E.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com