【题目】选修4-4：坐标系与参数方程
在平面直角坐标系
中，直线
的参数方程为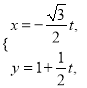
（
为参数），以原点为极点， 
轴正半轴为极轴建立极坐标系，曲线
的方程为
，定点
，点
是曲线
上的动点， 
为
的中点.
（1）求点
的轨迹
的直角坐标方程；
（2）已知直线
与
轴的交点为
，与曲线
的交点为
，若
的中点为
，求
的长.
中考解读考点精练系列答案科目：高中数学 来源： 题型：
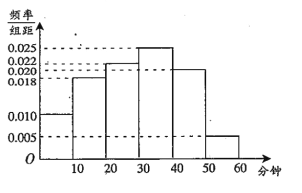
【题目】某中学为研究学生的身体素质与课外体育锻炼时间的关系，对该校200名学生的课外体育锻炼平均每天运动的时间（单位：分钟）进行调查，将收集的数据分成
六组，并作出频率分布直方图（如图），将日均课外体育锻炼时间不低于40分钟的学生评价为“课外体育达标”.
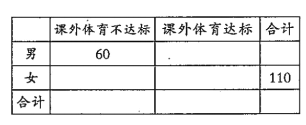
(1)请根据直方图中的数据填写下面的
列联表，并通过计算判断是否能在犯错误的概率不超过0.01的前提下认为“课外体育达标”与性别有关？
（2）现按照“课外体育达标”与“课外体育不达标”进行分层抽样，抽取8人，再从这8名学生中随机抽取3人参加体育知识问卷调查，记“课外体育不达标”的人数为
，求
的分布列和数学期望.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某高中一年级600名学生参加某次测评，根据男女学生人数比例，使用分层抽样的方法从中随机抽取了100名学生，记录他们的分数，将数据分成
组：[20,30），[30,40），┄，[80,90]，并整理得到如下频率分布直方图：
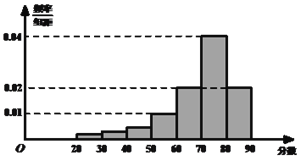
（1）从总体的600名学生中随机抽取一人，估计其分数小于70的概率；
（2）已知样本中分数小于40的学生有5人，试估计总体中分数在区间[40,50）内的人数；
（3）已知样本中有一半男生的分数不小于70，且样本中分数不小于70的男女生人数相等．试估计总体中男生和女生人数的比例．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如果函数f(x)＝
x3－x满足：对于任意的x1，x2∈[0,2]，都有|f(x1)－f(x2)|≤a2恒成立，则a的取值范围是( )
A. [－
， 
]
B. [－
， 
]
C. (－∞，－ 
]∪[
，＋∞)
D. (－∞，－ 
]∪[
，＋∞)
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图所示，向高为H的水瓶A，B，C，D同时以等速注水，注满为止；
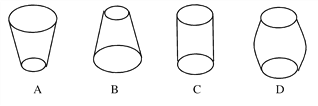
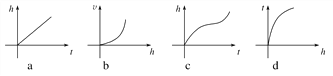
(1)若水深h与注水时间t的函数图象是下图中的a，则水瓶的形状是________；
(2)若水量ν与水深h的函数图像是下图中的b，则水瓶的形状是________；
(3)若水深h与注水时间t的函数图象是下图中的c，则水瓶的形状是________；
(4)若注水时间t与水深h的函数图象是下图中的d，则水瓶的形状是________。
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】定义在R上的单调函数f(x)满足f(2)＝
，且对任意x，y∈R，都有f(x＋y)＝f(x)＋f(y)．
(1)求证：f(x)为奇函数；
(2)若f(k·3x)＋f(3x－9x－2)<0对任意x∈R恒成立，求实数k的取值范围．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】数列
： 
满足： 
， 
或1（
）．对任意
，都存在
，使得
．，其中
且两两不相等．
(I)若
．写出下列三个数列中所有符合题目条件的数列的序号；
①1,1,1,2,2,2;②1,1,1,1,2,2,2,2;③1,l,1,1,1,2,2,2,2
(Ⅱ)记
．若
，证明： 
；
(Ⅲ)若
，求
的最小值.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图，已知椭圆
： 
的离心率为
，上、下顶点分别为
、
，点
在椭圆上，且异于点
、
，直线
、
与直线
： 
分别交于点
、
，且
面积的最大值为
.
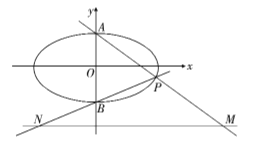
（1）求椭圆
的标准方程；
（2）求线段
的长的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
