
【题目】定义在R上的单调函数f(x)满足f(2)=![]() ,且对任意x,y∈R,都有f(x+y)=f(x)+f(y).
,且对任意x,y∈R,都有f(x+y)=f(x)+f(y).
(1)求证:f(x)为奇函数;
(2)若f(k·3x)+f(3x-9x-2)<0对任意x∈R恒成立,求实数k的取值范围.
 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案科目:高中数学 来源: 题型:
【题目】(本小题满分10分)一位网民在网上光顾某淘宝小店,经过一番浏览后,对该店铺中的![]() 五种商品有购买意向.已知该网民购买
五种商品有购买意向.已知该网民购买![]() 两种商品的概率均为
两种商品的概率均为![]() ,购买
,购买![]() 两种商品的概率均为
两种商品的概率均为![]() ,购买
,购买![]() 种商品的概率为
种商品的概率为![]() .假设该网民是否购买这五种商品相互独立.
.假设该网民是否购买这五种商品相互独立.
(1)求该网民至少购买4种商品的概率;
(2)用随机变量![]() 表示该网民购买商品的种数,求
表示该网民购买商品的种数,求![]() 的概率分布和数学期望.
的概率分布和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设p:f(x)=![]() 在区间(1,+∞)上是减函数;q:若x1,x2是方程x2-ax-2=0的两个实根,则不等式m2+5m-3≥|x1-x2|对任意实数a∈[-1,1]恒成立.若p不正确,q正确,求实数m的取值范围.
在区间(1,+∞)上是减函数;q:若x1,x2是方程x2-ax-2=0的两个实根,则不等式m2+5m-3≥|x1-x2|对任意实数a∈[-1,1]恒成立.若p不正确,q正确,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在平面直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为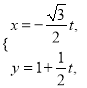 (
(![]() 为参数),以原点为极点,
为参数),以原点为极点, ![]() 轴正半轴为极轴建立极坐标系,曲线
轴正半轴为极轴建立极坐标系,曲线![]() 的方程为
的方程为![]() ,定点
,定点![]() ,点
,点![]() 是曲线
是曲线![]() 上的动点,
上的动点, ![]() 为
为![]() 的中点.
的中点.
(1)求点![]() 的轨迹
的轨迹![]() 的直角坐标方程;
的直角坐标方程;
(2)已知直线![]() 与
与![]() 轴的交点为
轴的交点为![]() ,与曲线
,与曲线![]() 的交点为
的交点为![]() ,若
,若![]() 的中点为
的中点为![]() ,求
,求![]() 的长.
的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在标准温度和大气压下,人体血液中氢离子的物质的量的浓度(单位mol/L,记作![]() )和氢氧根离子的物质的量的浓度(单位mol/L,记作
)和氢氧根离子的物质的量的浓度(单位mol/L,记作![]() )的乘积等于常数
)的乘积等于常数![]() .已知pH值的定义为
.已知pH值的定义为![]() ,健康人体血液的pH值保持在7.35~7.45之间,那么健康人体血液中的
,健康人体血液的pH值保持在7.35~7.45之间,那么健康人体血液中的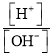 可以为(参考数据:
可以为(参考数据: ![]() ,
, ![]() )
)
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设动点![]() 到定点
到定点![]() 的距离比它到
的距离比它到![]() 轴的距离大
轴的距离大![]() ,记点
,记点![]() 的轨迹为曲线
的轨迹为曲线![]() .
.
(1)求点![]() 的轨迹方程;
的轨迹方程;
(2)若圆心在曲线![]() 上的动圆
上的动圆![]() 过点
过点![]() ,试证明圆
,试证明圆![]() 与
与![]() 轴必相交,且截
轴必相交,且截![]() 轴所得的弦长为定值.
轴所得的弦长为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若函数f(x)=sin2ax-![]() sin ax·cos ax-
sin ax·cos ax-![]() (a>0)的图象与直线y=b相切,并且切点的横坐标依次成公差为
(a>0)的图象与直线y=b相切,并且切点的横坐标依次成公差为![]() 的等差数列.
的等差数列.
(1)求a,b的值;
(2)若x0∈![]() ,且x0是y=f(x)的零点,试写出函数y=f(x)在
,且x0是y=f(x)的零点,试写出函数y=f(x)在![]() 上的单调增区间.
上的单调增区间.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com