
分析 (1)利用有理数指数幂的性质和运算法则求解.
(2)利用有立方和公式、有理数指数幂的性质和运算法则求解.
解答 解:(1)${0.064^{-\frac{1}{3}}}-{({-\frac{1}{8}})^0}+{16^{\frac{3}{4}}}+{0.25^{\frac{1}{2}}}+2{log_3}6-{log_3}$12
=$[(0.4)^{3}]^{-\frac{1}{3}}-1+({2}^{4})^{\frac{3}{4}}+0.5+lo{g}_{3}36$-log312
=(0.4)-1-1+8+0.5+log33
=2.5-1+8+0.5+1
=11.
(2)∵${a^{\frac{1}{2}}}+{a^{-\frac{1}{2}}}$=3,
∴$\frac{{{a^{\frac{3}{2}}}-{a^{-\frac{3}{2}}}}}{{{a^{\frac{1}{2}}}-{a^{-\frac{1}{2}}}}}$=$\frac{({a}^{\frac{1}{2}}-{a}^{-\frac{1}{2}})(a+1+{a}^{-1})}{{a}^{\frac{1}{2}}-{a}^{-\frac{1}{2}}}$
=a+a-1+1
=$({a}^{\frac{1}{2}}+{a}^{-\frac{1}{2}})^{2}$-2+1
=9-2+1
=8.
点评 本题考查有理数指数幂化简求值,是基础题,解题时要认真审题,注意立方和公式、有理数指数幂的性质和运算法则的合理运用.


科目:高中数学 来源:2017届湖南衡阳八中高三上学期月考二数学(文)试卷(解析版) 题型:填空题
函数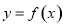 图象上不同两点
图象上不同两点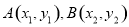 处的切线的斜率分别是
处的切线的斜率分别是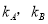 ,规定
,规定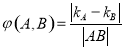 (
(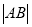 为线段AB的长度)叫做曲线
为线段AB的长度)叫做曲线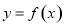 在点A与点B之间的“弯曲度”,给出以下命题:
在点A与点B之间的“弯曲度”,给出以下命题:
①函数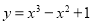 图象上两点A与B的横坐标分别为1和2,则
图象上两点A与B的横坐标分别为1和2,则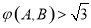 ;
;
②存在这样的函数,图象上任意两点之间的“弯曲度”为常数;
③设点A,B是抛物线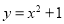 上不同的两点,则
上不同的两点,则 ;
;
④设曲线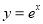 (e是自然对数的底数)上不同两点
(e是自然对数的底数)上不同两点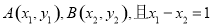 ,若
,若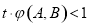 恒成立,则实数t的取值范围是
恒成立,则实数t的取值范围是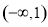 .
.
其中真命题的序号为________.(将所有真命题的序号都填上)
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源:2017届湖南衡阳八中高三上学期月考二数学(理)试卷(解析版) 题型:选择题
设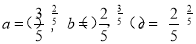 ,则a, b,c的大小关系是( )
,则a, b,c的大小关系是( )
A、a>c>b B、a>b>c
C、c>a>b D、b>c>a
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 命题“若x2+y2=0,则x=y=0”的逆否命题为“若x,y中至少有一个不为0,则x2+y2≠0” | |
| B. | 若命题$p:?{x_0}∈R,x_0^2-{x_0}+1≤0$,则¬p:?x∈R,x2-x+1>0 | |
| C. | 若向量$\overrightarrow a,\overrightarrow b$满足$\overrightarrow a•\overrightarrow b<0$,则$\overrightarrow a$与$\overrightarrow b$的夹角为钝角 | |
| D. | △ABC中,sinA>sinB是A>B的充要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|-1≤x<2} | B. | {-1,0,1} | C. | {0,1,2} | D. | {-1,1} |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com