Question

7．对于函数f（x），设k＞0，当x∈[a，b]时，其值域为[ka，kb]，称区间[a，b]为函数f（x）的k倍值区间．下列函数存在5倍值区间的是：②③④．（填序号）
①f（x）=5x+1；②$f（x）=-\frac{1}{2}{x^2}+2x$；③f（x）=x³；④f（x）=2^x；⑤f（x）=lgx．

Answer 1

分析 由题意，先判断函数的单调性，从而确定值域的求法，作图判断f（x）=2^x与f（x）=lgx即可．

解答 解：①∵f（x）=5x+1在其定义域上是单调增函数，
∴5a+1=5a，5b+1=5b，无解；
∴函数f（x）=5x+1不存在5倍值区间；
②若b≤2，则令-$\frac{1}{2}$b²+2b=5b，
解得，b=-6或b=0，
$f（x）=-\frac{1}{2}{x^2}+2x$存在5倍值区间[-6，0]；
③若f（x）=x³在其定义域上是单调增函数，
令x³=5x解得，
x=0，x=$\sqrt{5}$或x=-$\sqrt{5}$；
故f（x）=x³存在5倍值区间[-$\sqrt{5}$，0]；
④作函数f（x）=2^x与y=5x的图象如下，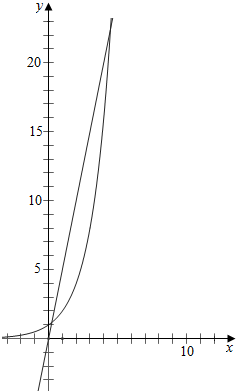

图象有两个交点，
故方程2^x=5x有两个不同的解，设为x₁，x₂，
故f（x）=2^x存在5倍值区间[x₁，x₂]．
⑤作函数f（x）=lgx与y=5x的图象如下，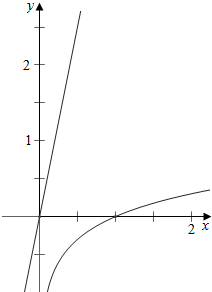
，
故函数f（x）=lgx不存在5倍值区间．
故答案为：②③④．

点评 本题考查了学生对新定义的接受与应用能力及数形结合的思想应用．