Question

4．若实数x、y、m满足|x-m|＜|y-m|，则称x比y接近m．
（1）若2x比1接近3，求x的取值范围；
（2）已知函数f（x）定义域D=（-∞，0）∪（0，1）∪（1，3）∪（3，+∞），对于任意的x∈D，f（x）等于x²-2x与x中接近0的那个值，写出函数f（x）的解析式，若关于x的方程f（x）-a=0有两个不同的实数根，求出a的取值范围；
（3）已知a，b∈R，m＞0且a≠b，求证：$\frac{a+mb}{m+1}$比$\sqrt{\frac{{{a^2}+m{b^2}}}{m+1}}$接近0．

Answer 1

分析 （1）直接根据定义，问题等价为|2x-3|＜|1-3|，解出即可；
（2）先求出函数f（x）的解析式并画出函数图象，再运用数形结合的方法，求a的取值范围；
（3）直接运用作差法比较两式的大小．

解答 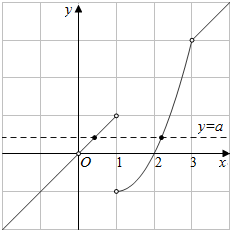解：（1）因为2x比1接近3，所以|2x-3|＜|1-3|，
即|2x-3|＜2，解得$\frac{1}{2}$＜x＜$\frac{5}{2}$，
所以，x的取值范围为：（$\frac{1}{2}$，$\frac{5}{2}$）；
（2）分类讨论如下：
①当x²-2x比x接近于0时，|x²-2x|＜|x|，
解得，x∈（1，3），
②当x比x²-2x接近于0时，|x²-2x|＞|x|，
解得，x∈（-∞，0）∪（0，1）∪（3，+∞），
所以，f（x）=$\left\{\begin{array}{l}{x^2-2x，x∈（1，3）}\\{x，x∈（-∞，0）∪（0，1）∪（3，+∞）}\end{array}\right.$，
画出f（x）的图象，如右图，
因为方程f（x）=a有两个实根，根据函数图象得，
a∈（-1，0）∪（0，1）；
（3）对两式$\frac{a+mb}{m+1}$，$\sqrt{\frac{{{a^2}+m{b^2}}}{m+1}}$平方作差得，
△=（$\sqrt{\frac{{{a^2}+m{b^2}}}{m+1}}$）²-（$\frac{a+mb}{m+1}$）2
=$\frac{（m+1）（a^2+mb^2）-（a+bm）^2}{（m+1）^2}$=$\frac{m（a-b）^2}{（m+1）^2}$，
因为a，b∈R，m＞0且a≠b，所以，△＞0恒成立，
所以，$\sqrt{\frac{{{a^2}+m{b^2}}}{m+1}}$＞|$\frac{a+mb}{m+1}$|，
即$\frac{a+mb}{m+1}$比$\sqrt{\frac{{{a^2}+m{b^2}}}{m+1}}$接近0．

点评 本题主要考查了绝对值不等式的解法，分段函数解析式的确定，和不等式的证明，体现了分类讨论，数形结合的解题思想，属于难题．