
分析 (1)有理数指数幂的性质、运算法则求解.
(2)利用对数性质、运算法则求解.
解答 解:(1)0.027${\;}^{-\frac{1}{3}}$-(-$\frac{1}{7}$)-2+256${\;}^{\frac{3}{4}}$-3-1+($\sqrt{2}$-1)0
=($\frac{1000}{27}$)${\;}^{\frac{1}{3}}$-(-7)2+${({2}^{8})}^{\frac{3}{4}-\frac{1}{3}+1}$
=$\frac{10}{3}-49+64-\frac{1}{3}+1$
=19.
(2)$\frac{lg8+lg125-lg2-lg5}{lg\sqrt{10}lg0.1}$
=$\frac{lg\frac{8×125}{2×5}}{lg1{0}^{\frac{1}{2}}lg1{0}^{-1}}$
=$\frac{lg1{0}^{2}}{\frac{1}{2}×(-1)}$
=-4.
点评 本题考查指数式、对数式化简求值,是基础题,解题时要认真审题,注意对数、有理数性质、运算法则及性质的合理运用.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|-1≤x<2} | B. | {-1,0,1} | C. | {0,1,2} | D. | {-1,1} |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源:2017届湖北襄阳四中高三七月周考三数学(文)试卷(解析版) 题型:解答题
选修4-1:几何证明选讲
如图所示,在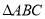 中,
中,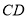 是
是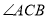 的角平分线,
的角平分线,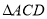 的外接圆交
的外接圆交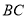 于
于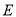 点.
点.
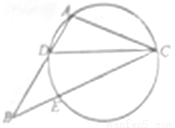
(1)证明: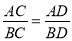 ;
;
(2)若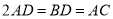 ,求
,求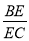 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com