
【题目】已知点F为椭圆![]() (a>b>0)的一个焦点,点A为椭圆的右顶点,点B为椭圆的下顶点,椭圆上任意一点到点F距离的最大值为3,最小值为1.
(a>b>0)的一个焦点,点A为椭圆的右顶点,点B为椭圆的下顶点,椭圆上任意一点到点F距离的最大值为3,最小值为1.
(1)求椭圆的标准方程;
(2)若M、N在椭圆上但不在坐标轴上,且直线AM∥直线BN,直线AN、BM的斜率分别为k1和k2,求证:k1k2=e2﹣1(e为椭圆的离心率).
【答案】(1)![]() (2)证明见解析
(2)证明见解析
【解析】
(1)根据椭圆上任意一点到点F距离的最大值为3,最小值为1,则有![]() 求解.
求解.
(2)由(1)可知,A(2,0),B(0,![]() ),分别设直线AM的方程为y=k(x﹣2),直线BN的方程为y=kx
),分别设直线AM的方程为y=k(x﹣2),直线BN的方程为y=kx![]() ,与椭圆方程联立,用韦达定理求得点M,N的坐标,再利用斜率公式代入k1k2求解.
,与椭圆方程联立,用韦达定理求得点M,N的坐标,再利用斜率公式代入k1k2求解.
(1)由题意可知,![]() ,解得
,解得![]() ,
,
∴b2=a2﹣c2=3,
∴椭圆的标准方程为:![]() ;
;
(2)由(1)可知,A(2,0),B(0,![]() ),
),
设直线AM的斜率为k,则直线BN的斜率也为k,
故直线AM的方程为y=k(x﹣2),直线BN的方程为y=kx![]() ,
,
由 得:(3+4k2)x2﹣16k2x+16k2﹣12=0,
得:(3+4k2)x2﹣16k2x+16k2﹣12=0,
∴![]() ,∴
,∴![]() ,
,![]() ,
,
∴ ,
,
由 得:
得:![]() ,
,
∴![]() ,
,![]() ,
,
∴ ,
,
∴ ,
,
 ,
,
∴k1k2
 ,
,
又∵![]() ,
,
∴k1k2=e2﹣1.


 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案科目:高中数学 来源: 题型:
【题目】某圆柱的高为2,底面周长为16,其三视图如图所示,圆柱表面上的点![]() 在正视图上的对应点为
在正视图上的对应点为![]() ,圆柱表面上的点
,圆柱表面上的点![]() 在左视图上的对应点为
在左视图上的对应点为![]() ,则在此圆柱侧面上,从
,则在此圆柱侧面上,从![]() 到
到![]() 的路径中,最短路径的长度为( )
的路径中,最短路径的长度为( )

A. ![]() B.
B. ![]() C.
C. ![]() D. 2
D. 2
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆锥的顶点为A,高和底面的半径相等,BE是底面圆的一条直径,点D为底面圆周上的一点,且∠ABD=60°,则异面直线AB与DE所成角的正弦值为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆锥的顶点为A,高和底面的半径相等,BE是底面圆的一条直径,点D为底面圆周上的一点,且∠ABD=60°,则异面直线AB与DE所成角的正弦值为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某城市在进行创建文明城市的活动中,为了解居民对“创建文明城”的满意程度,组织居民给活动打分(分数为整数,满分100分),从中随机抽取一个容量为120的样本,发现所给数据均在[40,100]内.现将这些分数分成以下6组并画出样本的频率分布直方图,但不小心污损了部分图形,如图所示.观察图形则下列说法中有错误的是( )
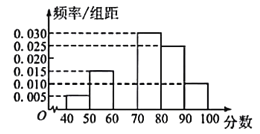
A.第三组的频数为18人
B.根据频率分布直方图估计众数为75分
C.根据频率分布直方图估计样本的平均数为75分
D.根据频率分布直方图估计样本的中位数为75分
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥S﹣ABCD中,侧面SCD为钝角三角形且垂直于底面ABCD,CD=SD,点M是SA的中点,AD//BC,∠ABC=90°,AB=AD![]() BC=a.
BC=a.
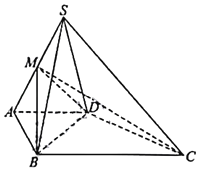
(1)求证:平面MBD⊥平面SCD;
(2)若∠SDC=120°,求三棱锥C﹣MBD的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂为提高生产效率,开展技术创新活动,提出了完成某项生产任务的两种新的生产方式.为比较两种生产方式的效率,选取40名工人,将他们随机分成两组,每组20人,第一组工人用第一种生产方式,第二组工人用第二种生产方式.根据工人完成生产任务的工作时间(单位:min)绘制了茎叶图:则下列结论中表述不正确的是
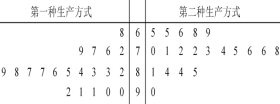
A. 第一种生产方式的工人中,有75%的工人完成生产任务所需要的时间至少80分钟
B. 第二种生产方式比第一种生产方式的效率更高
C. 这40名工人完成任务所需时间的中位数为80
D. 无论哪种生产方式的工人完成生产任务平均所需要的时间都是80分钟.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com