
【题目】函数![]() 的部分图象如图所示
的部分图象如图所示

(1)求![]() 的最小正周期及解析式;
的最小正周期及解析式;
(2)设![]() 求函数
求函数![]() 在区间
在区间![]() 上的最大值和最小值.
上的最大值和最小值.
【答案】(1) π, f(x)=sin(2x![]() );(2)最大值为1,最小值为
);(2)最大值为1,最小值为![]()
【解析】
(1)由图可知A=1,![]() ,从而可求ω;再由图象经过点(
,从而可求ω;再由图象经过点(![]() ,1),可求得φ;
,1),可求得φ;
(2)依题意g(x)=sin(2x![]() )﹣cos2x,化简整理为g(x)=sin(2x
)﹣cos2x,化简整理为g(x)=sin(2x![]() ),即可求得g(x)在区间
),即可求得g(x)在区间![]() 上的最大值和最小值及对应的x的集合.
上的最大值和最小值及对应的x的集合.
解:(1)由图可知:![]() ,A=1,
,A=1,
∴T=π,
∴ω![]() 2,
2,
∴f(x)=sin(2x+)
又∵图象经过点![]() ,
,
∴1=sin(2![]() φ),
φ),
∴![]() φ
φ![]() 2kπ,k∈Z,
2kπ,k∈Z,
∴φ![]() 2kπ,k∈Z,
2kπ,k∈Z,
又∵|φ|![]() ,
,
∴φ![]() ,
,
∴解析式为f(x)=sin(2x![]() );
);
(2)g(x)=f(x)﹣cos2x
=sin(2x![]() )﹣cos2x
)﹣cos2x
=sin2xcos![]() cos2xsin
cos2xsin![]() cos2x
cos2x
![]() sin2x
sin2x![]() cos2x
cos2x
=sin(2x![]() );
);
∵![]() ,∴2x
,∴2x![]() ,
,
当2x![]() ,即x=
,即x=![]() 时,g(x)有最大值为1,
时,g(x)有最大值为1,
当2x![]() ,即x=
,即x=![]() 时,g(x)有最大值为
时,g(x)有最大值为![]()


 精英口算卡系列答案
精英口算卡系列答案科目:高中数学 来源: 题型:
【题目】下列命题中,错误命题是
A. “若![]() ,则
,则![]() ”的逆命题为真
”的逆命题为真
B. 线性回归直线![]() 必过样本点的中心
必过样本点的中心![]()
C. 在平面直角坐标系中到点![]() 和
和![]() 的距离的和为
的距离的和为![]() 的点的轨迹为椭圆
的点的轨迹为椭圆
D. 在锐角![]() 中,有
中,有![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线![]() 与直线
与直线![]() 互相垂直,且交点为Q,点
互相垂直,且交点为Q,点![]() ,线段QF的垂直平分线与直线
,线段QF的垂直平分线与直线![]() 交于点P.
交于点P.
(I)若动点P的轨迹为曲线E,求曲线E的方程;
(Ⅱ)已知点![]()
![]() ,经过点M的两条直线分别与曲线E交于A,B和C,D,且
,经过点M的两条直线分别与曲线E交于A,B和C,D,且![]() ,设直线AC,BD的斜率分别为
,设直线AC,BD的斜率分别为![]()
![]() ,是否存在常数
,是否存在常数![]() ,使得当
,使得当![]() 变动时,
变动时,![]() ?说明理由.
?说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知a,b,c为正数,f(x)=|x+a|+|x+b|+|x﹣c|.
(1)若a=b=c=1,求函数f(x)的最小值;
(2)若f(0)=1且a,b,c不全相等,求证:b3c+c3a+a3b>abc.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点F为椭圆![]() (a>b>0)的一个焦点,点A为椭圆的右顶点,点B为椭圆的下顶点,椭圆上任意一点到点F距离的最大值为3,最小值为1.
(a>b>0)的一个焦点,点A为椭圆的右顶点,点B为椭圆的下顶点,椭圆上任意一点到点F距离的最大值为3,最小值为1.
(1)求椭圆的标准方程;
(2)若M、N在椭圆上但不在坐标轴上,且直线AM∥直线BN,直线AN、BM的斜率分别为k1和k2,求证:k1k2=e2﹣1(e为椭圆的离心率).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=log3(ax+b)的图象经过点A(2,1)和B(5,2),an=an+b(n∈N*).
(1)求{an};
(2)设数列{an}的前n项和为Sn,bn![]() ,求{bn}的前n项和Tn.
,求{bn}的前n项和Tn.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知有穷数列A:![]() (
(![]() 且
且![]() ).定义数列A的“伴生数列”B:
).定义数列A的“伴生数列”B:![]() ,其中
,其中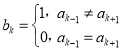 (
(![]() ),规定
),规定![]() ,
,![]() .
.
(1)写出下列数列的“伴生数列”:
①1,2,3,4,5;
②1,![]() ,1,
,1,![]() ,1.
,1.
(2)已知数列B的“伴生数列”C:![]() ,
,![]() ,…,
,…,![]() ,…,
,…,![]() ,且满足
,且满足![]() (
(![]() ,2,…,n).
,2,…,n).
(i)若数列B中存在相邻两项为1,求证:数列B中的每一项均为1;
(ⅱ)求数列C所有项的和.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com