
【题目】已知有穷数列A:![]() (
(![]() 且
且![]() ).定义数列A的“伴生数列”B:
).定义数列A的“伴生数列”B:![]() ,其中
,其中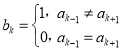 (
(![]() ),规定
),规定![]() ,
,![]() .
.
(1)写出下列数列的“伴生数列”:
①1,2,3,4,5;
②1,![]() ,1,
,1,![]() ,1.
,1.
(2)已知数列B的“伴生数列”C:![]() ,
,![]() ,…,
,…,![]() ,…,
,…,![]() ,且满足
,且满足![]() (
(![]() ,2,…,n).
,2,…,n).
(i)若数列B中存在相邻两项为1,求证:数列B中的每一项均为1;
(ⅱ)求数列C所有项的和.
【答案】(1)①1,1,1,1,1②1,0,0,0,1(2)(i)证明见解析(ⅱ)所有项的和![]() 或
或![]() (n是3的倍数)
(n是3的倍数)
【解析】
(1)根据“伴生数列”的定义求解即可;
(2)(i)设存在![]() ,使得
,使得![]() ,讨论
,讨论![]() 和
和![]() ,结合“伴生数列”的定义证明即可;
,结合“伴生数列”的定义证明即可;
(ⅱ)利用反证法得出不可能存在![]() ,
,![]() ,再对数列
,再对数列![]() 的前三项
的前三项![]() ,
,![]() ,
,![]() 的值进行讨论,当
的值进行讨论,当![]() 时,得出所有项的和
时,得出所有项的和![]() ;当
;当![]() ,
,![]() ,
,![]() 时,得出
时,得出![]() 与已知矛盾;当
与已知矛盾;当![]() ,
,![]() ,
,![]() 时,结合“伴生数列”的定义得出所有项的和
时,结合“伴生数列”的定义得出所有项的和![]() ,同理可以得出当
,同理可以得出当![]() ,
,![]() ,
,![]() 及
及![]() ,
,![]() ,
,![]() 时,所有项的和
时,所有项的和![]() .
.
解:(1)①1,1,1,1,1;
②1,0,0,0,1.
(2)(i)由题意,存在![]() ,使得
,使得![]() .
.
若![]() ,即
,即![]() 时,
时,![]() .
.
于是![]() ,
,![]() .
.
所以![]() ,所以
,所以![]() .即
.即![]() .
.
依次类推可得![]() (
(![]() ,3,…,
,3,…,![]() ).
).
所以![]() (
(![]() ,2,…,n).
,2,…,n).
若![]() ,由
,由![]() 得
得![]() .
.
于是![]() .所以
.所以![]() .
.
依次类推可得![]() .
.
所以![]() (
(![]() ,2,…,n).
,2,…,n).
综上可知,数列B中的每一项均为1.
(ⅱ)首先证明不可能存在![]() 使得
使得![]() .
.
若存在![]() 使得
使得![]() ,
,
则![]() .
.
又![]() 得
得![]() 与已知矛盾.
与已知矛盾.
所以不可能存在![]() ,
,![]() .
.
由此及(ⅰ)得数列![]() 的前三项
的前三项![]() ,
,![]() ,
,![]() 的可能情况如下:
的可能情况如下:
当![]() 时,由(i)可得
时,由(i)可得![]() (
(![]() ,2,…,n).
,2,…,n).
于是![]() (
(![]() ,2,…,n)
,2,…,n)![]() .
.
所以所有项的和![]() .
.
当![]() ,
,![]() ,
,![]() 时,
时,![]() ,
,
此时![]() 与已知矛盾.
与已知矛盾.
当![]() ,
,![]() ,
,![]() 时,
时,![]() ,
,![]() ,
,![]() .
.
于是![]() ,
,![]() .
.
故![]() ,
,![]() ,
,![]()
于是![]() ,
,![]() ,
,![]() ,
,
于是![]() ,
,![]() ,
,![]() ,且
,且![]() ,
,![]() ,
,![]() .
.
依次类推![]() 且n恰是3的倍数满足题意.
且n恰是3的倍数满足题意.
所以所有项的和![]() .
.
同理可得![]() ,
,![]() ,
,![]() 及
及![]() ,
,![]() ,
,![]() 时,
时,
当且仅当n恰是3的倍数时,满足题意.
此时所有项的和![]() .
.
综上,所有项的和![]() 或
或![]() (n是3的倍数).
(n是3的倍数).


科目:高中数学 来源: 题型:
【题目】如图,在四棱锥S﹣ABCD中,侧面SCD为钝角三角形且垂直于底面ABCD,CD=SD,点M是SA的中点,AD//BC,∠ABC=90°,AB=AD![]() BC=a.
BC=a.
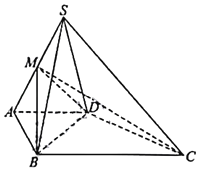
(1)求证:平面MBD⊥平面SCD;
(2)若∠SDC=120°,求三棱锥C﹣MBD的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,直线l的参数方程为![]() (t为参数),若以O为极点,x轴的正半轴为极轴且取相同的单位长度建立极坐标系,曲线C的极坐标方程为
(t为参数),若以O为极点,x轴的正半轴为极轴且取相同的单位长度建立极坐标系,曲线C的极坐标方程为![]() .
.
(1)求曲线C的直角坐标方程及直线l的普通方程;
(2)将所得曲线C向右平移1个单位长度,再将曲线C上的所有点的横坐标变为原来的2倍,得到曲线![]() ,求曲线
,求曲线![]() 上的点到直线l的距离的最大值.
上的点到直线l的距离的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如果对某对象连续实施两次变换后的结果就是变换前的对象,那么我们称这种变换为“回归”变换.如:对任意一个实数,变换:取其相反数.因为相反数的相反数是它本身,所以变换“取实数的相反数”是一种“回归”变换.有下列3种变换:
①对![]() ,变换:求集合A的补集;
,变换:求集合A的补集;
②对任意![]() ,变换:求z的共轭复数;
,变换:求z的共轭复数;
③对任意![]() ,变换:
,变换:![]() (k,b均为非零实数).
(k,b均为非零实数).
其中是“回归”变换的是______.
查看答案和解析>>
科目:高中数学 来源: 题型:
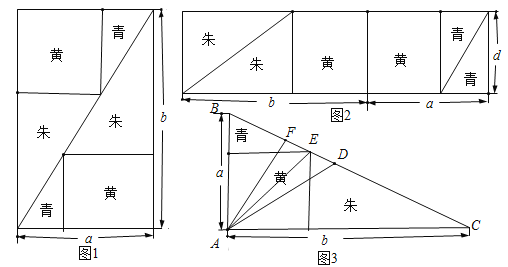
【题目】《九章算术》中“勾股容方”问题:“今有勾五步,股十二步,问勾中容方几何?”魏晋时期数学家刘徽在其《九章算术注》中利用出入相补原理给出了这个问题的一般解法:如图1,用对角线将长和宽分别为![]() 和
和![]() 的矩形分成两个直角三角形,每个直角三角形再分成一个内接正方形(黄)和两个小直角三角形(朱、青).将三种颜色的图形进行重组,得到如图2所示的矩形.该矩形长为
的矩形分成两个直角三角形,每个直角三角形再分成一个内接正方形(黄)和两个小直角三角形(朱、青).将三种颜色的图形进行重组,得到如图2所示的矩形.该矩形长为![]() ,宽为内接正方形的边长
,宽为内接正方形的边长![]() .由刘徽构造的图形还可以得到许多重要的结论,如图3.设
.由刘徽构造的图形还可以得到许多重要的结论,如图3.设![]() 为斜边
为斜边![]() 的中点,作直角三角形
的中点,作直角三角形![]() 的内接正方形对角线
的内接正方形对角线![]() ,过点
,过点![]() 作
作![]() 于点
于点![]() ,则下列推理正确的是( )
,则下列推理正确的是( )
①由图1和图2面积相等得![]() ;
;
②由![]() 可得
可得![]() ;
;
③由![]() 可得
可得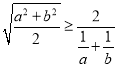 ;
;
④由![]() 可得
可得![]() .
.
A.①②③④B.①②④C.②③④D.①③
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂为提高生产效率,开展技术创新活动,提出了完成某项生产任务的两种新的生产方式.为比较两种生产方式的效率,选取40名工人,将他们随机分成两组,每组20人,第一组工人用第一种生产方式,第二组工人用第二种生产方式.根据工人完成生产任务的工作时间(单位:min)绘制了茎叶图:则下列结论中表述不正确的是
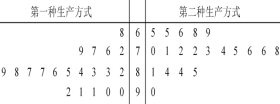
A. 第一种生产方式的工人中,有75%的工人完成生产任务所需要的时间至少80分钟
B. 第二种生产方式比第一种生产方式的效率更高
C. 这40名工人完成任务所需时间的中位数为80
D. 无论哪种生产方式的工人完成生产任务平均所需要的时间都是80分钟.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的普通方程为:
的普通方程为:![]() ,以坐标原点为极点,
,以坐标原点为极点,![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() ,正方形
,正方形![]() 的顶点都在
的顶点都在![]() 上,且
上,且![]() 逆时针依次排列,点
逆时针依次排列,点![]() 的极坐标为
的极坐标为![]()
(1)写出曲线![]() 的参数方程,及点
的参数方程,及点![]() 的直角坐标;
的直角坐标;
(2)设![]() 为椭圆
为椭圆![]() 上的任意一点,求:
上的任意一点,求:![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了实施“科技下乡,精准脱贫”战略,某县科技特派员带着![]() 三个农业扶贫项目进驻某村,对仅有的四个贫困户进行产业帮扶.经过前期走访得知,这四个贫困户甲、乙、丙、丁选择
三个农业扶贫项目进驻某村,对仅有的四个贫困户进行产业帮扶.经过前期走访得知,这四个贫困户甲、乙、丙、丁选择![]() 三个项目的意向如下:
三个项目的意向如下:
扶贫项目 |
|
|
|
贫困户 | 甲、乙、丙、丁 | 甲、乙、丙 | 丙、丁 |
若每个贫困户只能从自己已登记的选择意向中随机选取一项,且每个项目至多有两个贫困户选择,则甲乙两户选择同一个扶贫项目的概率为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com