考点:异面直线及其所成的角,直线与平面垂直的性质
专题:空间角
分析:(1)连结AC、BD,交点为O,连结,OD1,ON,易证AC⊥平面D1DO,即可证得EN⊥A1C1.
(2)取DC的中点F,连结A1F,C1F,则∠A1C1F就是异面直线A1C1与ED所成角,解三角形用余弦定理求得即可.
解答:
(1)证明:连结AC、BD,交点为O,连结,OD
1,ON,则
D1EON,∴四边形D
1ONE是平行四边形,∴D
1O∥EN,
∵AC⊥BD,AC⊥DD
1,BD∩DD
1=D,∴AC⊥平面D
1DO,
∵D
1O?平面D
1DO,∴AC⊥D
1O,
∵A
1C
1∥AC,D
1O∥EN,
∴EN⊥A
1C
1.
(2)解:取DC的中点F,连结A
1F,C
1F,
∵
EC1DF,∴四边形EDFC
1是平行四边形,∴ED∥C
1F,
∴∠A
1C
1F就是异面直线A
1C
1与ED所成角.
设正方体的棱长为2,则
A1C1=2,
C1F=,A
1F=3,
∴cos∠A
1C
1F=
=
=
.
∴异面直线A
1C
1与ED所成角的余弦值是
.
点评:本题主要考查空间中的线面关系的证明及异面直线所成角的求法等知识,考查学生线面垂直定理及平移法作异面直线所成角以及余弦定理的应用,属于中档题.

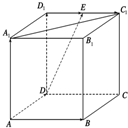 如图所示,在正方体ABCD-A1B1C1D1中,E为D1C1的中点,N为BC的中点.
如图所示,在正方体ABCD-A1B1C1D1中,E为D1C1的中点,N为BC的中点.
