
分析 首先利用有向线段的坐标求法分别求出向量$\overrightarrow{AB}$和$\overrightarrow{AC}$的坐标,然后利用数量积公式求夹角的余弦值.
解答 解:由已知$\overrightarrow{OA}$=(1,1,0),$\overrightarrow{OB}$=(4,1,0),$\overrightarrow{OC}$=(4,5,-1),得到向量$\overrightarrow{AB}$=(3,0,0),$\overrightarrow{AC}$=(3,4,-1),
所以向量$\overrightarrow{AB}$和$\overrightarrow{AC}$的夹角的余弦值为$\frac{\overrightarrow{AB}•\overrightarrow{AC}}{|\overrightarrow{AB}||\overrightarrow{AC}|}$=$\frac{3×3+0+0}{3×\sqrt{{3}^{2}+{4}^{2}+{1}^{2}}}=\frac{3\sqrt{26}}{26}$;
故答案为:$\frac{{3\sqrt{26}}}{26}$.
点评 本题考查了有向线段的坐标以及利用数量积公式求空间向量的夹角;属于基础题.


 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案科目:高中数学 来源: 题型:选择题
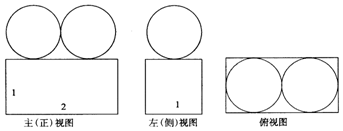
| A. | 2+$\frac{4π}{3}$ | B. | 2+$\frac{π}{3}$ | C. | 1+$\frac{4π}{3}$ | D. | 10+8π |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$|$\overrightarrow{AB}$|•|$\overrightarrow{AC}$| | B. | $\frac{1}{2}$$|\begin{array}{l}{{x}_{1}}&{{y}_{1}}&{1}\\{{x}_{2}}&{{y}_{2}}&{1}\\{{x}_{3}}&{{y}_{3}}&{1}\end{array}|$ | ||
| C. | $\frac{1}{2}$|$\overrightarrow{AB}$$•\overrightarrow{AC}$| | D. | $\frac{1}{2}$(cos|$\overrightarrow{AB}$|•|$\overrightarrow{AC}$|) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 12种 | B. | 14种 | C. | 16种 | D. | 24种 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com