
| A. | $\frac{5}{19}$ | B. | $\frac{1}{19}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{2}$ |
分析 求出从经过初试的20人中任选2人的所有不同方法种数,再分类求出选到第二人与公司所需专业不对口的选法种数,利用古典概型概率计算公式得答案.
解答 解:从经过初试的20人中任选2人,共有${A}_{20}^{2}$=20×19种不同选法.
第一个人面试后,则选到的第二人与公司所需专业不对口的选法分为两类:
第一类、第一个人与公司专业对口的选法为${C}_{15}^{1}{C}_{5}^{1}$;
第二类、第一个人与公司专业不对口的选法为${C}_{5}^{1}{C}_{4}^{1}$.
故第一个人面试后,选到第二人与公司所需专业不对口的选法共15×5+5×4=19×5.
∴选取的第二人与公司所需专业不对口的概率是$\frac{19×5}{20×19}=\frac{1}{4}$.
故选:C.
点评 本题考查古典概型概率计算公式的应用,对题意理解是关键,属中档题.


科目:高中数学 来源: 题型:选择题
| A. | 4π | B. | 8π | C. | 16π | D. | 32π |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2016 | B. | 1008 | C. | 504 | D. | 2017 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
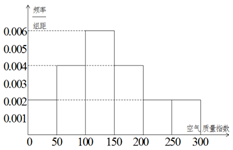 某中学的环保社团参照国家环境标准制定了该校所在区域空气质量指数与空气质量等级对应关系如表(假设该区域空气质量指数不会超过300):
某中学的环保社团参照国家环境标准制定了该校所在区域空气质量指数与空气质量等级对应关系如表(假设该区域空气质量指数不会超过300):| 空气质量指数 | (0,50] | (50,100] | (100,150] | (150,200] | (200,250] | (250,300] |
| 空气质量等级 | 1级优 | 2级良 | 3级轻度 污染 | 4级中度 污染 | 5级重度 污染 | 6级严重污染 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{9}{16}$ | B. | $\frac{7}{16}$ | C. | $\frac{9}{32}$ | D. | $\frac{7}{32}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 上网时间(分钟) | [30,40) | [40,50) | [50,60) | [60,70) | [70,80] |
| 人数 | 5 | 25 | 30 | 25 | 15 |
| 上网时间(分钟) | [30,40) | [40,50) | [50,60) | [60,70) | [70,80] |
| 人数 | 10 | 20 | 40 | 20 | 10 |
| 上网时间少于60分钟 | 上网时间不少于60分钟 | 合计 | |
| 男生 | 60 | 40 | 100 |
| 女生 | 70 | 30 | 100 |
| 合计 | 130 | 70 | 200 |
| P(K2≥k0) | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.84 | 5.024 | 6.635 | 7.879 | 10.83 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com