
分析 (Ⅰ)由题意可得${S_n}={n^2}$,然后再由an=Sn-Sn-1(n≥2)求数列的通项公式;
(Ⅱ)把(Ⅰ)中所求的通项公式代入数列$\{\frac{1}{{{a_n}{a_{n+1}}}}\}$,利用裂项相消法求其和,再代入${T_n}>\frac{100}{209}$求最小正整数n.
解答 解:(Ⅰ)∵点(n,Sn)均在函数y=f(x)上的图象上,∴${S_n}={n^2}$,
当n=1时,a1=1,
当n≥2时,${a_n}={S_n}-{S_{n-1}}={n^2}-{(n-1)^2}=2n-1$,
经检验当n=1时,也满足an=2n-1,
∴an=2n-1;
(Ⅱ)∵an=2n-1,
∴${T_n}=\frac{1}{{{a_1}{a_2}}}+\frac{1}{{{a_2}{a_3}}}+…+\frac{1}{{{a_{n-1}}{a_n}}}$=$\frac{1}{1×3}+\frac{1}{3×5}+\frac{1}{5×7}+…+\frac{1}{{({2n-1})({2n+1})}}$
=$\frac{1}{2}[(\frac{1}{1}-\frac{1}{3})+(\frac{1}{3}-\frac{1}{5})+(\frac{1}{5}-\frac{1}{7})+…+(\frac{1}{2n-1}-\frac{1}{2n+1})]$
=$\frac{1}{2}({1-\frac{1}{2n+1}})$=$\frac{n}{2n+1}$,
由${T_n}=\frac{n}{2n+1}>\frac{100}{209}$,得$n>\frac{100}{9}$,
∴满足${T_n}>\frac{100}{209}$的最小正整数为12.
点评 本题考查数列的函数特性,考查了数列递推式,训练了裂项相消法求数列的通项公式,是中档题.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源:2017届重庆市高三理上适应性考试一数学试卷(解析版) 题型:选择题
记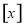 表示不超过
表示不超过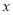 的最大整数,如
的最大整数,如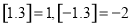 .设函数
.设函数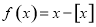 ,若方程
,若方程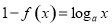 有且仅有3个实数根,则正实数
有且仅有3个实数根,则正实数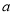 的取值范围为( )
的取值范围为( )
A.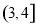 B.
B.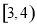 C.
C. D.
D.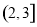
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
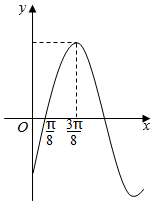 函数f(x)=Asin(ωx-$\frac{π}{4}$)(A>0,ω>0)的部分图象如图所示.
函数f(x)=Asin(ωx-$\frac{π}{4}$)(A>0,ω>0)的部分图象如图所示.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | $\frac{4}{3}$ | C. | 6 | D. | $\frac{3}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{2}{3}$ | D. | $\frac{11}{12}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com