练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    已知实数x，y满足不等式组
    x-y≤2
    x+y≤4
    x≥2
    ，则z=2x+y的最小值是（　　）
    A、2B、4C、6D、7
    考点：简单线性规划
    专题：不等式的解法及应用
    分析：作出不等式组对应的平面区域，利用z的几何意义，即可得到结论．
    解答： 试题分析：做出可行域，
    解：作出不等式组对应的平面区域如图：
    由z=2x+y得y=-2x+z，
    平移直线y=-2x+z，
    由图象可知当直线y=-2x+z经过点A时，直线的截距最小，
    此时z最小，
    由
    x=2
    x-y=2
    ，解得
    x=2
    y=0
    ，
    即A（2，0），此时z=2×2+0=4，
    故选：B
    点评：本题主要考查线性规划的应用，利用z的几何意义，利用数形结合是解决本题的关键．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    已知sin（π+α）=
    2
    3
    ，求sin（π-α）-cot（α-π）cos（3π+α）的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    如图，有一块边长为1（百米）的正方形区域ABCD，在点A处有一个可转动的探照灯，其照射角∠PAQ始终为45n（其中点P，Q分别在边BC，CD上），设∠PAB=θ，tanθ=t．
    （1）用t表示出PQ的长度，并探求△CPQ的周长l是否为定值．
    （2）问探照灯照射在正方形ABCD内部区域阴影部分的面积S最大为多少（平方百米）？

    查看答案和解析>>

    科目：高中数学 来源： 题型：

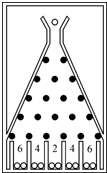    在一块倾斜放置的矩形木块上钉着一个形如“等腰三角形”的五行铁钉，钉子之间留有空隙作为通道，自上而下第1行2个铁钉之间有1个空隙，第2行3个铁钉之间有2个空隙…第5行6个铁钉之间有5个空隙（如图）．某人将一个玻璃球从第1行的空隙向下滚动，玻璃球碰到第2行居中的铁钉后以相等的概率滚入第2行的左空隙或右空隙，以后玻璃球按类似方式继续往下滚动，落入第5行的某一个空隙后，掉入木板下方相应的球槽．玻璃球落入不同球槽得到的分数ξ如图所示．
    （Ⅰ）求Eξ；
    （Ⅱ）若此人进行4次相同试验，求至少3次获得4分的概率．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知定义在R上的函数y=f（x）满足f（x+1）=f（x-1），当-1＜x≤1时，f（x）=x3，若函数g（x）=f（x）-loga|x|恰好有6个零点，则a有取值范围是（　　）
    A、a∈[
    1
    5
    ，
    1
    3
    ]∪[3，5]
    B、a∈[0，
    1
    5
    ]∪[5，+∞]
    C、a∈[
    1
    7
    ，
    1
    5
    ]∪[5，7]
    D、(
    1
    7
    ，
    1
    5
    )

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    若函数的反函数为f-1（x）=log3x，则f（x）=
     
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    直线l：y=-
    		3
    x+1的倾斜角α=
     
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知命题p：若xy≠4，则x≠1或y≠4，命题q：对任意实数x有x2-x+1＞0，则（　　）
    A、“p或￢q”为假命题
    B、“￢p且q”为真命题
    C、“￢p或q”为假命题
    D、“p且q”为真命题

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知函数f（x）=lnx-ax，a∈R．
    （Ⅰ）若曲线y=f（x）在任意点处的切线的倾斜角都是锐角，求a的取值范围；
    （Ⅱ）若函数f（x）在区间（
    1
    e
    ，e）内有零点，求a的取值范围．

    查看答案和解析>>

    同步练习册答案