
为增强市民的环境保护意识,面向全市征召义务宣传志愿者.现从符合条件的志愿者中随机抽取100名按年龄分组:第1组 ,第2组
,第2组 ,第3组
,第3组 ,第4组
,第4组 ,第5组
,第5组 ,得到的频率分布直方图如图所示.若从第3,4,5组中用分层抽样的方法抽取6名志愿者参广场的宣传活动,并决定在这6名志愿者中随机抽取2名志愿者介绍宣传经验,则第4组至少有一名志愿者被抽中的概率为( )
,得到的频率分布直方图如图所示.若从第3,4,5组中用分层抽样的方法抽取6名志愿者参广场的宣传活动,并决定在这6名志愿者中随机抽取2名志愿者介绍宣传经验,则第4组至少有一名志愿者被抽中的概率为( )

A. B.
B.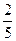 C.
C. D.
D.
C
【解析】第3组的人数为0.3×100=30, 第4组的人数为0.2×100=20, 第5组的人数为0.1×100=10.
因为第3,4,5组共有60名志愿者,所以利用分层抽样的方法在60名志愿者中抽取6名志愿者,每组抽取的人数分别为:第3组: ×6=3; 第4组:
×6=3; 第4组: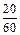 ×6=2; 第5组:
×6=2; 第5组: ×6=1.
×6=1.
所以应从第3,4,5组中分别抽取3人,2人,1人.
记第3组的3名志愿者为A1,A2,A3,第4组的2名志愿者为B1,B2,第5组的1名志愿者为C1.
则从6名志愿者中抽取2名志愿者有:
(A1,A2), (A1,A3),(A1,B1),(A1,B2),(A1,C1),(A2,A3),(A2,B1),(A2,B2),(A2,C1),(A3,B1),(A3,B2),
(A3,C1),(B1,B2),(B1,C1),(B2,C1),共有15种.其中第4组的2名志愿者B1,B2至少有一名志愿者被抽中的有:
(A1,B1), (A1,B2), (A2,B1), (A2,B2), (A3,B1), (A3,B2), (B1,B2), (B1,C1), (B2,C1),共有9种,
所以第4组至少有一名志愿者被抽中的概率为 .故选C.
.故选C.


科目:高中数学 来源:2014高考名师推荐数学理科全称量词与存在性量词(解析版) 题型:选择题
已知命题p1:函数y=2x-2-x在R上为增函数,p2:函数y=2x+2-x在R上为减函数,则在命题q1:p1∨p2,q2:p1∧p2,q3:(?p1)∨p2和q4:p1∧(?p2)中,真命题是
A. q1,q3
B. q2,q3
C. q1,q4
D. q2,q4
查看答案和解析>>
科目:高中数学 来源:2014高考名师推荐数学理科不等式选讲(解析版) 题型:解答题
已知函数f(x)=|x-a|,其中a>1.
(1)当a=2时,求不等式f(x)≥4-|x-4|的解集;
(2)已知关于x的不等式|f(2x+a)-2f(x)|≤2的解集为{x|1≤x≤2},求a的值.
查看答案和解析>>
科目:高中数学 来源:2014高考名师推荐数学文空间线面平行、面面平行、线面垂直、面面垂直(解析版) 题型:选择题
设m,n是两条不同的直线,α,β是两个不同的平面,下列命题中正确的是( )
A.若α⊥β,m?α,n?β,则m⊥n
B.若α∥β,m?α,n?β,则m∥n
C.若m⊥n,m?α,n?β,则α⊥β
D.若m⊥α,m∥n,n∥β,则α⊥β
查看答案和解析>>
科目:高中数学 来源:2014高考名师推荐数学文科预测题(解析版) 题型:解答题
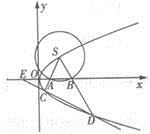
如图, 是抛物线为
是抛物线为 上的一点,以S为圆心,r为半径(
上的一点,以S为圆心,r为半径( )做圆,分别交x轴于A,B两点,连结并延长SA、SB,分别交抛物线于C、D两点。
)做圆,分别交x轴于A,B两点,连结并延长SA、SB,分别交抛物线于C、D两点。
(1)求证:直线CD的斜率为定值;
(2)延长DC交x轴负半轴于点E,若EC : ED = 1 : 3,求 的值。
的值。
查看答案和解析>>
科目:高中数学 来源:2014高考名师推荐数学文科预测题(解析版) 题型:填空题
如图,AB是⊙O的一条切线,切点为B,ADE、CFD都是⊙O的割线,AC=AB.
(1)证明:AC2=AD·AE
(2)证明:FG∥AC

查看答案和解析>>
科目:高中数学 来源:2014高考名师推荐数学文科预测题(解析版) 题型:解答题
已知函数f(x)=ex+2x2—3x
(1)求曲线y=f(x)在点(1,f(1))处的切线方程;
(2) 当x ≥1时,若关于x的不等式f(x)≥ax恒成立,求实数a的取值范围;
(3)求证函数f(x)在区间[0,1)上存在唯一的极值点,并用二分法求函数取得极值时相应x的近似值(误差不超过0.2);(参考数据e≈2.7,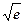 ≈1.6,e0.3≈1.3)。
≈1.6,e0.3≈1.3)。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com