
| A. | |z1|<0且|z2|<1 | B. | |z1|<1或|z2|<1 | C. | |z1|=1且|z2|=1 | D. | |z1|=1或|z2|=1 |
分析 利用$|z{|}^{2}=z•\overline{z}$,结合$|{z}_{1}-\overline{{z}_{2}}{|}^{2}=|1-{z}_{1}{z}_{2}{|}^{2}$,化简出$|{z}_{1}{|}^{2}+|{z}_{2}{|}^{2}-1-|\overline{{z}_{1}}{|}^{2}|\overline{{z}_{2}}{|}^{2}=0$,通过分解因式推出z1,z2中至少又一个值为1可得答案.
解答 解:由|z1-$\overline{{z}_{2}}$|=|1-z1z2|,得
$|{z}_{1}-\overline{{z}_{2}}{|}^{2}=|1-{z}_{1}{z}_{2}{|}^{2}$,即$({z}_{1}-\overline{{z}_{2}})(\overline{{z}_{1}-\overline{{z}_{2}}})$=$(1-{z}_{1}{z}_{2})(\overline{1-{z}_{1}{z}_{2}})$,
∴$({z}_{1}-\overline{{z}_{2}})(\overline{{z}_{1}}-{z}_{2})$=$(1-{z}_{1}{z}_{2})(1-\overline{{z}_{1}}\overline{{z}_{2}})$,
∴$|{z}_{1}{|}^{2}-{z}_{1}{z}_{2}-\overline{{z}_{1}}\overline{{z}_{2}}+|{z}_{2}{|}^{2}$=$1-\overline{{z}_{1}}\overline{{z}_{2}}-{z}_{1}{z}_{2}+|\overrightarrow{{z}_{1}}{|}^{2}|\overline{{z}_{2}}{|}^{2}$.
∴$|{z}_{1}{|}^{2}+|{z}_{2}{|}^{2}-1-|\overline{{z}_{1}}{|}^{2}|\overline{{z}_{2}}{|}^{2}=0$,
即$(|{z}_{1}{|}^{2}-1)(|{z}_{2}{|}^{2}-1)=0$.
得$|{z}_{1}{|}^{2}=1$或$|{z}_{2}{|}^{2}=1$.
∴|z1|=1或|z2|=1.
故选:D.
点评 本题考查了复数代数形式的乘除运算,考查了复数的基本概念,考查了推理能力与计算能力,属于中档题.


 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,1) | B. | (0,+∞) | C. | (1,+∞) | D. | (0,1)∪(1,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{3}$ | B. | $\frac{2π}{3}$ | C. | $\frac{5π}{6}$ | D. | $\frac{π}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
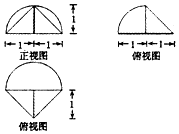
| A. | $\frac{5π}{6}$ | B. | $\frac{5π}{3}$ | C. | $\frac{π+1}{3}$ | D. | $\frac{2π+1}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(3)>e2f(1) | B. | f(3)<ef(2) | C. | f(4)<e4f(0) | D. | f(4)<e5f(-1) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 学生编号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 数学分数x | 60 | 65 | 70 | 75 | 80 | 85 | 90 | 95 |
| 物理分数y | 72 | 77 | 80 | 84 | 88 | 90 | 93 | 95 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com