
| A. | (0,1) | B. | (0,+∞) | C. | (1,+∞) | D. | (0,1)∪(1,+∞) |
分析 构造函数g(x)=f(x)-lnx-$\frac{{x}^{2}}{2}$,根据函数的单调性求出g(x)的单调性,从而求出答案.
解答 解:不等式$\frac{f(x)-lnx}{x^2}>\frac{1}{2}$等价于f(x)>lnx+$\frac{{x}^{2}}{2}$,
构造函数g(x)=f(x)-lnx-$\frac{{x}^{2}}{2}$,
∴g′(x)=f′(x)-$\frac{1}{x}$-x,
∵不等式$f'(x)≤\frac{1}{x}+x$的解集为(0,1],
∴g(x)≤0,在(0,1)上恒成立,
∴g′(x)在(0,1]上单调递减,
∴g(x)在(1,+∞)上单调递增,
∴g(x)min=g(1)=f(1)-ln1-$\frac{1}{2}$=0,
∴g(x)>0的解集为(0,1)∪(1,+∞)
故选:D
点评 本题考查了函数的单调性、最值问题,考查导数的应用,是一道中档题.


科目:高中数学 来源: 题型:选择题
| A. | A>B | B. | sin2A>sin2B | C. | cos2A<cos2B | D. | a>b |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 大前提错误 | B. | 小前提错误 | C. | 推理形式错误 | D. | 结论正确 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充分必要条件 | D. | 即不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|x=$\frac{kπ}{2}$+$\frac{π}{8}$,k∈Z} | B. | {x|x=kπ+$\frac{π}{8}$,k∈Z} | C. | {x|x=$\frac{kπ}{2}$+$\frac{π}{4}$,k∈Z} | D. | {x|x=kπ+$\frac{π}{4}$,k∈Z} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | |z1|<0且|z2|<1 | B. | |z1|<1或|z2|<1 | C. | |z1|=1且|z2|=1 | D. | |z1|=1或|z2|=1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
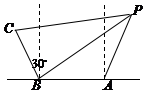 为捍卫钓鱼岛及其附属岛屿的领土主权,中国派出舰船“唐山号”、“石家庄号”和“邯郸号”在钓鱼岛领海巡航.某日,正巡逻在A处的“唐山号”突然发现来自P处的疑似敌舰的某信号,发现信号时“石家庄号”和“邯郸号”正分别位于如图所示的B、C两处,其中A在B的正东方向相距6海里处,C在B的北偏西30°方向相距4海里处.由于B、C比A距P更远,因此,4秒后B、C才同时发现这一信号(该信号的传播速度为每秒1海里),试确定疑似敌舰相对于A点“唐山号”的位置.
为捍卫钓鱼岛及其附属岛屿的领土主权,中国派出舰船“唐山号”、“石家庄号”和“邯郸号”在钓鱼岛领海巡航.某日,正巡逻在A处的“唐山号”突然发现来自P处的疑似敌舰的某信号,发现信号时“石家庄号”和“邯郸号”正分别位于如图所示的B、C两处,其中A在B的正东方向相距6海里处,C在B的北偏西30°方向相距4海里处.由于B、C比A距P更远,因此,4秒后B、C才同时发现这一信号(该信号的传播速度为每秒1海里),试确定疑似敌舰相对于A点“唐山号”的位置.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com