
分析 (1)两边取正切列方程解出x,从而可求出arccos$\frac{x}{2}$的值;
(2)两边取正切得出tana关于x的函数,利用不等式得出tana的范围,从而得出a的范围;
(3)根据二次函数的性质列不等式组得出tana的范围,利用根与系数的关系得出α+β的最值.
解答 解:(1)当$a=\frac{π}{4}$时,arctan$\frac{x}{2}$+arctan(2-x)=$\frac{π}{4}$,
∴$\frac{\frac{x}{2}+(2-x)}{1-\frac{x}{2}•(2-x)}=1$,解得x=-1或x=2,
∴当x=-1时,$arccos\frac{x}{2}$=arccos(-$\frac{1}{2}$)=π-arccos$\frac{1}{2}$=$\frac{2π}{3}$;
当x=2时,arccos$\frac{x}{2}$=arccos1=0,
(2)∵$arctan\frac{x}{2}+arctan(2-x)=a$,
∴tana=$\frac{\frac{x}{2}+(2-x)}{1-\frac{x}{2}(2-x)}$=$\frac{4-x}{{x}^{2}-2x+2}$
当x=4时,tana=0,
当x≠4时,tana=$\frac{1}{4-x+\frac{10}{4-x}-6}$,
∵4-x+$\frac{10}{4-x}$≥2$\sqrt{10}$或4-x+$\frac{10}{4-x}$≤-2$\sqrt{10}$,
∴0<tana≤$\frac{1}{2\sqrt{10}-6}$或$\frac{1}{-2\sqrt{10}-6}$≤tana<0,
综上,$\frac{1}{-2\sqrt{10}-6}$≤tana≤$\frac{1}{2\sqrt{10}-6}$,
∴a∈$[arctan\frac{1}{{-2\sqrt{10}-6}},arctan\frac{1}{{2\sqrt{10}-6}}]$.
(3)由(2)知$\frac{4-x}{{x}^{2}-2x+2}$=tana在[5,15]上有两解α,β,
即tana•x2+(1-2tana)x+2tana-4=0在[5,15]有两解α,β,
∴α+β=$\frac{2tana-1}{tana}$=2-$\frac{1}{tana}$,
∴△=(1-2tana)2-8tana(tana-2)=-4tan2a+12tana+1>0,解得$\frac{3-\sqrt{10}}{2}$<tana<$\frac{3+\sqrt{10}}{2}$且tana≠0.
①若tana>0,则对称轴$\frac{2tana-1}{2tana}$=1-$\frac{1}{2tana}$<1,方程在[5,15]上不可能有两解,不符合题意,舍去;
②若tana<0,令5<1-$\frac{1}{2tana}$<15,解得-$\frac{1}{8}$<tana<-$\frac{1}{28}$,
又$\left\{\begin{array}{l}{25tana+5(1-2tana)+2tana-4≤0}\\{225tana+15(1-2tana)+2tana-4≤0}\end{array}\right.$,解得tana≤-$\frac{1}{17}$,
综上,$\frac{3-\sqrt{10}}{2}$<tana≤-$\frac{1}{17}$,
∴当tana=-$\frac{1}{17}$时,α+β取得最大值2+17=19.
点评 本题考查了反三角函数的应用,二次函数的性质,属于中档题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,1) | B. | (0,+∞) | C. | (1,+∞) | D. | (0,1)∪(1,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
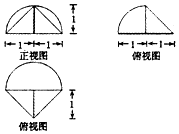
| A. | $\frac{5π}{6}$ | B. | $\frac{5π}{3}$ | C. | $\frac{π+1}{3}$ | D. | $\frac{2π+1}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(3)>e2f(1) | B. | f(3)<ef(2) | C. | f(4)<e4f(0) | D. | f(4)<e5f(-1) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 学生编号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 数学分数x | 60 | 65 | 70 | 75 | 80 | 85 | 90 | 95 |
| 物理分数y | 72 | 77 | 80 | 84 | 88 | 90 | 93 | 95 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2k+1项 | B. | 2k项 | C. | k+1项 | D. | k项 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com