
| A. | 2k+1项 | B. | 2k项 | C. | k+1项 | D. | k项 |
分析 首先分析题目证明不等式1+$\frac{1}{2}$+$\frac{1}{3}$+$\frac{1}{4}$+…+$\frac{1}{{2}^{n+1}-1}$>$\frac{n+1}{2}$(n∈N*),假设n=k时成立,求当n=k+1时,左端增加的项数.故可以分别把n=k+1,n=k代入不等式左边,使它们相减即可求出项数.
解答 解:当n=k时不等式为:1+$\frac{1}{2}$+$\frac{1}{3}$+$\frac{1}{4}$+…+$\frac{1}{{2}^{k+1}-1}$>$\frac{k+1}{2}$(k∈N*)成立
当n=k+1时不等式左边为1+$\frac{1}{2}$+$\frac{1}{3}$+$\frac{1}{4}$+…+$\frac{1}{{2}^{k+1}-1}$+$\frac{1}{{2}^{k+1}}+\frac{1}{{2}^{k+1}+1}+…+\frac{1}{{2}^{k+2}-1}$>$\frac{k+2}{2}$,
则左边增加2k+2-1-2k+1+1=2k+1项.
故选:A.
点评 本题主要考查用数学归纳法证明不等式的问题,属于概念性问题,计算量小,属于基础题目.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{6}$ | B. | $\frac{π}{3}$ | C. | $\frac{5π}{6}$ | D. | $\frac{2π}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
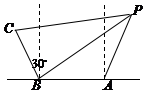 为捍卫钓鱼岛及其附属岛屿的领土主权,中国派出舰船“唐山号”、“石家庄号”和“邯郸号”在钓鱼岛领海巡航.某日,正巡逻在A处的“唐山号”突然发现来自P处的疑似敌舰的某信号,发现信号时“石家庄号”和“邯郸号”正分别位于如图所示的B、C两处,其中A在B的正东方向相距6海里处,C在B的北偏西30°方向相距4海里处.由于B、C比A距P更远,因此,4秒后B、C才同时发现这一信号(该信号的传播速度为每秒1海里),试确定疑似敌舰相对于A点“唐山号”的位置.
为捍卫钓鱼岛及其附属岛屿的领土主权,中国派出舰船“唐山号”、“石家庄号”和“邯郸号”在钓鱼岛领海巡航.某日,正巡逻在A处的“唐山号”突然发现来自P处的疑似敌舰的某信号,发现信号时“石家庄号”和“邯郸号”正分别位于如图所示的B、C两处,其中A在B的正东方向相距6海里处,C在B的北偏西30°方向相距4海里处.由于B、C比A距P更远,因此,4秒后B、C才同时发现这一信号(该信号的传播速度为每秒1海里),试确定疑似敌舰相对于A点“唐山号”的位置.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | $\sqrt{2}$ | C. | $\sqrt{3}$ | D. | $\sqrt{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $?{x_0}∈[{0,+∞}),{2^{x_0}}≥{x_0}^2$ | B. | $?{x_0}∈({-∞,0}),{2^{x_0}}≥{x_0}^2$ | ||
| C. | ?x∈(-∞,0),2x≥x2 | D. | ?x∈[0,+∞),2x<x2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com