
分析 (1)根据正弦定理与两角和的正弦公式,化简题中的等式可得sin(B+C)-2sinAcosC,结合三角函数的诱导公式算出cosC=$\frac{1}{2}$,可得角C的大小;
(2)由余弦定理可得ab的值,利用三角形面积公式即可求解.
解答 解:(1)∵在△ABC中,(2a-b)cosC-ccosB=0,
∴由正弦定理,可得sinCcosB=(2sinA-sinB)cosC,
即sinCcosB+sinBcosC=2sinAcosC,所以sin(B+C)=2sinAcosC,
∵△ABC中,sin(B+C)=sin(π-A)=sinA>0,
∴sinA=2sinAcosC,即sinA(1-2cosC)=0,可得cosC=$\frac{1}{2}$.
又∵C是三角形的内角,∴C=$\frac{π}{3}$.
(2)∵C=$\frac{π}{3}$,a+b=10,c=6,
∴由余弦定理可得:62=a2+b2-2abcosC=a2+b2-ab=(a+b)2-3ab=102-3ab,解得:ab=$\frac{64}{3}$,
∴S△ABC=$\frac{1}{2}$absinC=$\frac{1}{2}$×$\frac{64}{3}$×$\frac{\sqrt{3}}{2}$=$\frac{16\sqrt{3}}{3}$.
点评 本题求角C的大小并依此求三角形面积的最大值.着重考查了正余弦定理、两角和的正弦公式三角函数的图象性质,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(3)>e2f(1) | B. | f(3)<ef(2) | C. | f(4)<e4f(0) | D. | f(4)<e5f(-1) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 学生编号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 数学分数x | 60 | 65 | 70 | 75 | 80 | 85 | 90 | 95 |
| 物理分数y | 72 | 77 | 80 | 84 | 88 | 90 | 93 | 95 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -16 | B. | -8 | C. | 16 | D. | 8 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2k+1项 | B. | 2k项 | C. | k+1项 | D. | k项 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
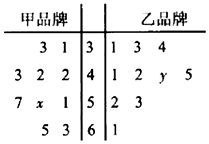 某商场对甲、乙两种品牌的牛奶进行为期100天的营销活动,为调查这100天的日销售情况,用简单随机抽样抽取10天进行统计,以它们的销售数量(单位:件)作为样本,样本数据的茎叶图如图.已知该样本中,甲品牌牛奶销量的平均数为48件,乙品牌牛奶销量的中位数为43件,将日销量不低于50件的日期称为“畅销日”.
某商场对甲、乙两种品牌的牛奶进行为期100天的营销活动,为调查这100天的日销售情况,用简单随机抽样抽取10天进行统计,以它们的销售数量(单位:件)作为样本,样本数据的茎叶图如图.已知该样本中,甲品牌牛奶销量的平均数为48件,乙品牌牛奶销量的中位数为43件,将日销量不低于50件的日期称为“畅销日”.| 畅销日天数 | 非畅销日天数 | 合计 | |
| 甲 | 50 | 50 | 100 |
| 乙 | 30 | 70 | 100 |
| 合计 | 80 | 120 | 200 |
| P(K2≥k0) | 0.050 | 0.010 | 0.001 |
| k0 | 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 33 | B. | 32 | C. | 35 | D. | 34 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com