
分析 先求出所有可能的事件的总数,及事件A,事件B,事件AB包含的基本事件个数,代入条件概率计算公式,可得答案
解答 解:设事件A为“蓝色骰子的点数为4或6“的概率为P(A)=$\frac{1}{3}$,
两颗骰子的点数之和大干8的6+3,6+4,6+5,6+6,3+6,4+6,5+6,5+5,4+5,5+4
事件B为“两颗骰子的点数之和大干8”的概率P(B)=$\frac{10}{36}$=$\frac{5}{12}$,$\frac{\frac{5}{36}}{\frac{1}{3}}$
∴事件A发生时,事件B发生的概率P(B|A)=$\frac{P(AB)}{P(A)}$=$\frac{\frac{5}{36}}{\frac{1}{3}}$=$\frac{5}{12}$,
故答案为:$\frac{5}{12}$.
点评 本题考查条件概率,条件概率有两种做法,本题采用事件发生所包含的事件数之比来解出结果.


科目:高中数学 来源: 题型:选择题
| A. | ① | B. | ②③ | C. | ①④ | D. | ①②③④ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,1) | B. | (0,+∞) | C. | (1,+∞) | D. | (0,1)∪(1,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
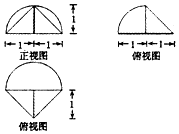
| A. | $\frac{5π}{6}$ | B. | $\frac{5π}{3}$ | C. | $\frac{π+1}{3}$ | D. | $\frac{2π+1}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2k+1项 | B. | 2k项 | C. | k+1项 | D. | k项 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com