练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】已知椭圆C：（）的焦距为4，其短轴的两个端点与长轴的一个端点构成正三角形.

    （1）求椭圆C的标准方程；

    （2）设F为椭圆C的左焦点，T为直线上任意一点，过F作TF的垂线交椭圆C于点P，Q.

    （i）证明：OT平分线段PQ（其中O为坐标原点）；

    （ii）当最小时，求点T的坐标.

    【答案】(1)；（2）证明见解析，

    【解析】

    （1）由题意，又，由此可求出的值，从而求得椭圆的方程.（2）椭圆方程化为.设PQ的方程为，代入椭圆方程得：.（ⅰ）设PQ的中点为，求出，只要，即证得OT平分线段PQ.（ⅱ）可用表示出PQ，TF可得：化简得：.再根据取等号的条件，可得T的坐标.

    （1），又.

    （2）椭圆方程化为.

    （ⅰ）设PQ的方程为，代入椭圆方程得：.

    设PQ的中点为，则

    又TF的方程为，则得，

    所以，即OT过PQ的中点，即OT平分线段PQ.

    （ⅱ），又，所以

    .

    当时取等号，此时T的坐标为.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】某城市交通部门为了对该城市共享单车加强监管，随机选取了100人就该城市共享单车的推行情况进行问卷调查，并将问卷中的这100人根据其满意度评分值（百分制）按照分成5组，制成如图所示频率分直方图.

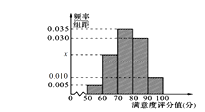
    （1）求图中x的值；

    （2）求这组数据的平均数和中位数；

    （3）已知满意度评分值在内的男生数与女生数3:2，若在满意度评分值为的人中随机抽取2人进行座谈，求2人均为男生的概率.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图,在四棱锥中,平面,底面为菱形,且,E为的中点.

    (1)求证:平面平面;

    (2)棱上是否存在点F,使得平面?说明理由.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在多面体中，四边形是正方形，平面平面，.

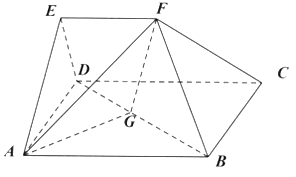
    （1）求证：平面；

    （2）在线段上是否存在点，使得平面与平面所成的锐二面角的大小为，若存在，求出的值；若不存在，说明理由.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】关于曲线，有如下结论：

    ①曲线C关于原点对称；

    ②曲线C关于直线x±y=0对称；

    ③曲线C是封闭图形，且封闭图形的面积大于2π；

    ④曲线C不是封闭图形，且它与圆x2+y2=2无公共点；

    ⑤曲线C与曲线有4个交点，这4点构成正方形．其中所有正确结论的序号为__．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图在四棱锥中,底面为矩形,,,平面平面,为等腰直角三角形,且,为底面的中心.

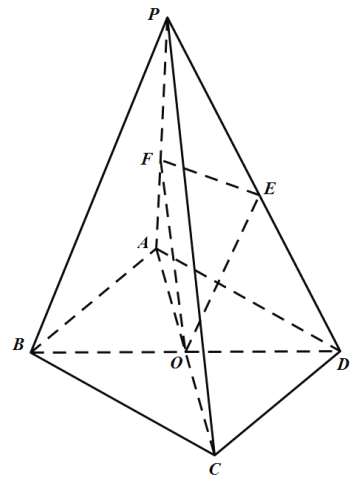
    (1)求异面直线与所成角的余弦值;

    (2)若为中点,在棱上,若,,且二面角的正弦值为,求实数的值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，四棱锥P-ABCD中，底面ABCD为矩形，PD⊥平面ABCD，点E、F分别是AB和PC的中点．

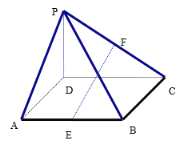
    (1)求证：AB⊥平面PAD；

    (2)求证：EF//平面PAD．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设椭圆的离心率为，椭圆上一点到左右两个焦点的距离之和是4.

    （1）求椭圆的方程；

    （2）已知过的直线与椭圆交于两点，且两点与左右顶点不重合，若，求四边形面积的最大值。

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】河道上有一抛物线型拱桥，在正常水位时，拱圈最高点距水面8m，拱圈内水面宽24m，一条船在水面以上部分高6.5m，船顶部宽6m．

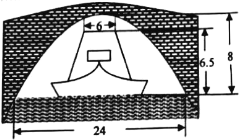
    （1）试建立适当的直角坐标系，求拱桥所在的抛物线的标准方程；

    （2）近日水位暴涨了1.54m，为此，必须加重船载，降低船身，才能通过桥洞，试问：船身至少应该降低多少?（精确到0.1m）

    查看答案和解析>>

    同步练习册答案