
分析 (1)利用等差数列的通项公式及其前n项和公式即可得出.
(2)分组求和即可得出.
解答 解:(1)由已知条件:$\left\{\begin{array}{l}{a_2}={a_1}+d=5\\{S_4}=4{a_1}+\frac{4×3}{2}×d=28\end{array}\right.$,
∴$\left\{\begin{array}{l}{a_1}=1\\ d=4.\end{array}\right.$,
∴an=a1+(n-1)×d=4n-3.
(2)由(1)可得${b_n}={(-1)^n}{a_n}={(-1)^n}({4n-3})$,
T2n=-1+5-9+13-17+…+(8n-3)=4×n=4n.
点评 本题考查了等差数列的通项公式及其前n项和公式,考查了推理能力与计算能力,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | $\frac{2}{9}$ | B. | $\frac{1}{3}$ | C. | $\frac{4}{9}$ | D. | $\frac{2}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
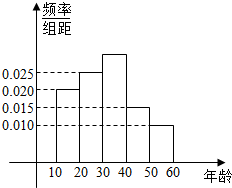 某市在“国际禁毒日”期间,连续若干天发布了“珍爱生命,原理毒品”的电视公益广告,期望让更多的市民知道毒品的危害性,禁毒志愿者为了了解这则广告的宣传效果,随机抽取了100名年龄阶段性在[10,20),[20,30),[30,40),[40,50),[50,60)的市民进行问卷调查,由此得到样本频率分布直方图如图所示.
某市在“国际禁毒日”期间,连续若干天发布了“珍爱生命,原理毒品”的电视公益广告,期望让更多的市民知道毒品的危害性,禁毒志愿者为了了解这则广告的宣传效果,随机抽取了100名年龄阶段性在[10,20),[20,30),[30,40),[40,50),[50,60)的市民进行问卷调查,由此得到样本频率分布直方图如图所示.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ($\frac{3}{2}$)n-1 | B. | 2n-1 | C. | ($\frac{2}{3}$)n-1 | D. | $\frac{1}{3}$($\frac{1}{{2}^{n-1}}$-1) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com