
| 价格x | 14 | 16 | 18 | 20 | 22 |
| 需求量y | 12 | 10 | 7 | 5 | 3 |
分析 根据所给的数据,做出变量x,y的平均数,求出回归模型的相关系数,可判断回归模型拟合效果的好坏.
解答 解:∵$\overline{x}$=$\frac{1}{5}$(14+16+18+20+22)=18,
$\overline{y}$=$\frac{1}{5}$(12+10+7+5+3)=7.4,
∴$\sum_{i=1}^{5}$xiyi=620,$\sum_{i=1}^{5}$${{x}_{i}}^{2}$=1660,
∴b=-1.15,a=$\overline{y}$-b$\overline{x}$=28.1.
∴线性回归方程为y=-1.15x+28.1;
x=14时,y=12,差是0,
x=16时,y=9.7,差是0.3,
x=18时,y=7.4,差是0.4,
x=20时,y=5.1,差是0.1,
x=22时,y=2.8,差是0.2,
∴R2=1-(0+0.09+0.16+0.01+0.04)÷(21.16+6.76+0.16+5.76+19.36)=1-0.0056391=0.9943609,
由于0.9943609非常接近1,
故这个回归模型拟合效果比较好.
点评 本题考查线性回归方程,考查最小二乘法,考查预报值的求法,是一个新课标中出现的新知识点,已经在广东的高考卷中出现过类似的题目.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
 如图,在正三棱柱ABC-A1B1C1(底面为正三角形且侧棱垂直于底面的三棱柱)中,底面边长AB=3,侧棱AA1=4,AC1与A1C相交于点E,点D是BC的中点.
如图,在正三棱柱ABC-A1B1C1(底面为正三角形且侧棱垂直于底面的三棱柱)中,底面边长AB=3,侧棱AA1=4,AC1与A1C相交于点E,点D是BC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
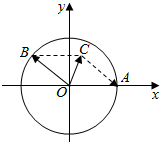 如图,在xoy平面上,点A(1,0),点B在单位圆上,∠AOB=θ(0<θ<π)
如图,在xoy平面上,点A(1,0),点B在单位圆上,∠AOB=θ(0<θ<π)查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
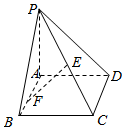 如图,在四棱锥中P-ABCD,底面ABCD为边长为$\sqrt{2}$的正方形,PA⊥BD.
如图,在四棱锥中P-ABCD,底面ABCD为边长为$\sqrt{2}$的正方形,PA⊥BD.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
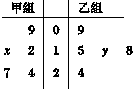 如图茎叶图记录了甲.乙两组各五名学生在一次英语听力测试中的成绩(单位:分)已知甲组数据的中位数为15,乙组数据的平均数为16.8,则x,y的值分别为5,8.
如图茎叶图记录了甲.乙两组各五名学生在一次英语听力测试中的成绩(单位:分)已知甲组数据的中位数为15,乙组数据的平均数为16.8,则x,y的值分别为5,8.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com