
分析 由$2{a}_{1}+{2}^{2}{a}_{2}$+…+2nan=$\frac{n(n-3)}{2}$,利用递推关系可得:n≥2时,${a}_{n}=\frac{n-2}{{2}^{n}}$;n=1时,a1=-1.通过作差可得数列的单调性.
解答 解:∵$2{a}_{1}+{2}^{2}{a}_{2}$+…+2nan=$\frac{n(n-3)}{2}$,
∴n≥2时,$2{a}_{1}+{2}^{2}{a}_{2}$+…+2n-1an-1=$\frac{(n-1)(n-4)}{2}$,
可得:2nan=$\frac{n(n-3)}{2}$-$\frac{(n-1)(n-4)}{2}$=n-2,
∴${a}_{n}=\frac{n-2}{{2}^{n}}$,
n=1时,a1=-1.
∴an=$\left\{\begin{array}{l}{-1,n=1}\\{\frac{n-2}{{2}^{n}},n≥2}\end{array}\right.$.
∵n=1时,a1=-1,a2=0.
n≥2时,an+1-an=$\frac{n-1}{{2}^{n+1}}$-$\frac{n-2}{{2}^{n}}$=$\frac{3-n}{{2}^{n+1}}$,
∴n=2时,a2<a3;n=3时,a3=a4;n≥4时,an+1<an,
因此:a1<a2<a3=a4>a5>…,
∴当n=3或4时,an取得最大值,a3=a4=$\frac{1}{8}$.
∵存在n∈N*,使得an≥m成立,则m$≤\frac{1}{8}$.
故答案为:$m≤\frac{1}{8}$.
点评 本题考查了数列的递推关系、不等式的性质,考查了分类讨论方法、推理能力与计算能力,属于中档题.


 优等生题库系列答案
优等生题库系列答案 53天天练系列答案
53天天练系列答案科目:高中数学 来源: 题型:解答题
| 价格x | 14 | 16 | 18 | 20 | 22 |
| 需求量y | 12 | 10 | 7 | 5 | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | “x>2”是”x2-x-2>0”必要条件 | B. | “$\overrightarrow{a}$•$\overrightarrow{b}$=0”是“$\overrightarrow{a}$⊥$\overrightarrow{b}$”充要条件 | ||
| C. | ?x∈R,x2+$\frac{1}{{{x^2}+1}}$≥1 | D. | ?x∈R,cosx+sinx>2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
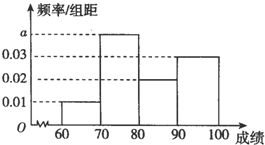 某校高三学生有两部分组成,应届生与复读生共2000学生,期末考试数学成绩换算为100分的成绩如图所示,从高三的学生中,利用分层抽样,抽取100名学生的成绩绘制成频率分布直方图:
某校高三学生有两部分组成,应届生与复读生共2000学生,期末考试数学成绩换算为100分的成绩如图所示,从高三的学生中,利用分层抽样,抽取100名学生的成绩绘制成频率分布直方图:查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1-$\sqrt{2}$ | B. | 1+$\sqrt{2}$ | C. | 3+2$\sqrt{2}$ | D. | 1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com