
 ijУ����ѧ������������ɣ�Ӧ�����븴������2000ѧ������ĩ������ѧ�ɼ�����Ϊ100�ֵijɼ���ͼ��ʾ���Ӹ�����ѧ���У����÷ֲ��������ȡ100��ѧ���ijɼ����Ƴ�Ƶ�ʷֲ�ֱ��ͼ��
ijУ����ѧ������������ɣ�Ӧ�����븴������2000ѧ������ĩ������ѧ�ɼ�����Ϊ100�ֵijɼ���ͼ��ʾ���Ӹ�����ѧ���У����÷ֲ��������ȡ100��ѧ���ijɼ����Ƴ�Ƶ�ʷֲ�ֱ��ͼ������ ��1����Ϊ��ȡ��Ӧ�����븴�����ı�Ϊ9�s1�����Ӧ������ȡ90�ˣ���������ȡ10�ˣ��ɴ���ȷ��ȷ������Ӧ�����븴������������
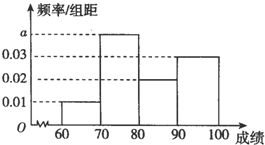
��2����Ƶ�ʷֲ�ͼ��С�������֮��Ϊ1����a=0.04���ɴ�������˴���ѧ�ɼ���ƽ���֣�
��3������Ƶ�ʷֲ�ֱ��ͼ��֪��ȡ�ĸ������������ֱ�Ϊ2��3�˳�ȡ��[80��90��������Ϊ��������Σ���֪��=0��1��2���ֱ������Ӧ�ĸ��ʣ��ɴ�������εķֲ���������ֵ��
��� �⣺��1���߳�ȡ��Ӧ�����븴�����ı�Ϊ9�s1��
��Ӧ������ȡ90�ˣ���������ȡ10�ˣ�
Ӧ����������Ϊ90��20=1800��������������Ϊ2000-1800=200��
��2��10����0.01+a+0.02+0.03��=1����a=0.04��
ƽ����Ϊ10����0.01��65+0.04��75+0.02��85+0.03��95��=82
��3������Ƶ�ʷֲ�ֱ��ͼ��֪����ȡ��[80��90����[90��100]��ѧ���ֱ�Ϊ100��0.2=20��100��0.3=30��
��ȡ�ĸ������������ֱ�Ϊ2��3��
��ȡ��[80��90��������Ϊ��������Σ���֪��=0��1��2��
��֪$p����=0��=\frac{C_3^2}{C_5^2}=\frac{3}{10}$��
$p����=1��=\frac{C_2^1C_3^1}{C_5^2}=\frac{3}{5}$��
$p����=2��=\frac{C_2^2}{C_5^2}=\frac{1}{10}$��
��εķֲ���Ϊ��
| �� | 0 | 1 | 2 |
| p | $\frac{3}{10}$ | $\frac{3}{5}$ | $\frac{1}{10}$ |
���� ���⿼��Ƶ�ʷֲ�ֱ��ͼ��Ӧ�ã�������ɢ����������ķֲ��к���ѧ�����������е��⣬����ʱҪ�������⣬ע���������֪ʶ�ĺ������ã�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��ֲ���Ҫ���� | B�� | ��Ҫ��������� | ||
| C�� | ��Ҫ���� | D�� | �Ȳ����Ҳ����Ҫ���� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | [-1��+�ޣ� | B�� | ��-�ޣ�0�� | C�� | ��-1��0] | D�� | [-1��0�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 1 | B�� | -1+$\sqrt{3}$i | C�� | -1 | D�� | $\sqrt{3}$i |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
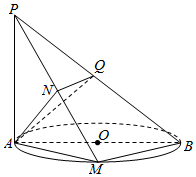 ��ͼ��ABΪ��O��ֱ����PA��ֱ�ڡ�O���ڵ�ƽ�棬MΪԲ��������һ�㣬AN��PM��NΪ���㣮
��ͼ��ABΪ��O��ֱ����PA��ֱ�ڡ�O���ڵ�ƽ�棬MΪԲ��������һ�㣬AN��PM��NΪ���㣮�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com