
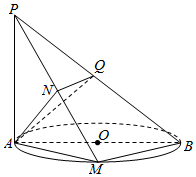
 如图,AB为⊙O的直径,PA垂直于⊙O所在的平面,M为圆周上任意一点,AN⊥PM,N为垂足.
如图,AB为⊙O的直径,PA垂直于⊙O所在的平面,M为圆周上任意一点,AN⊥PM,N为垂足.分析 (1)由PA⊥平面ABM得PA⊥BM,结合BM⊥AM得出BM⊥平面PAM,于是BM⊥AN,又AN⊥PM,得出AN⊥平面PBM;
(2)由AN⊥平面PBM得AN⊥PB,又PB⊥AQ得出PB⊥平面ANQ,于是NQ⊥PB.
解答 证明:(1)∵PA⊥平面ABM,BM?平面ABM,
∴PA⊥BM,
∵AB是⊙O的直径,M在⊙O上,
∴BM⊥AM,
又AM,PA?平面PAM,PA∩AM=A,
∴BM⊥平面PAM,∵AN?平面PAM,
∴AN⊥BM,又AN⊥PM,PM,BM?平面PBM,PM∩BM=M,
∴AN⊥平面PBM.
(2)∵AN⊥平面PBM,PB?平面PBM,
∴AN⊥PB,又AQ⊥PB,AN,AQ?平面ANQ,AN∩AQ=A,
∴PB⊥平面ANQ.∵NQ?平面ANQ,
∴PB⊥NQ.
点评 本题考查了线面垂直的判定与性质,属于中档题.


科目:高中数学 来源: 题型:解答题
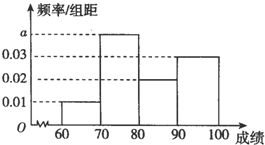 某校高三学生有两部分组成,应届生与复读生共2000学生,期末考试数学成绩换算为100分的成绩如图所示,从高三的学生中,利用分层抽样,抽取100名学生的成绩绘制成频率分布直方图:
某校高三学生有两部分组成,应届生与复读生共2000学生,期末考试数学成绩换算为100分的成绩如图所示,从高三的学生中,利用分层抽样,抽取100名学生的成绩绘制成频率分布直方图:查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1-$\sqrt{2}$ | B. | 1+$\sqrt{2}$ | C. | 3+2$\sqrt{2}$ | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | $\sqrt{2}$ | D. | 任意正数 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{n}{2n+1}$ | B. | $\frac{n}{2n+1}$ | C. | -$\frac{2n}{2n+1}$ | D. | $\frac{2n}{2n+1}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com