
| A. | -$\frac{n}{2n+1}$ | B. | $\frac{n}{2n+1}$ | C. | -$\frac{2n}{2n+1}$ | D. | $\frac{2n}{2n+1}$ |
分析 设等差数列{an}的公差为d(d≠0),运用等比数列的中项的性质和等差数列的通项公式和求和公式,解方程可得d=-1,a1=-$\frac{1}{2}$,可得an=-$\frac{2n-1}{2}$,即有$\frac{1}{(2n+1){a}_{n}}$=-$\frac{2}{(2n-1)(2n+1)}$=-($\frac{1}{2n-1}$-$\frac{1}{2n+1}$),运用数列的求和方法:裂项相消求和,化简即可得到所求和.
解答 解:设等差数列{an}的公差为d(d≠0),
S1,S2,S4成等比数列,且${a_3}=-\frac{5}{2}$,
可得S22=S1S4,a1+2d=-$\frac{5}{2}$,
即有(2a1+d)2=a1(4a1+6d),
化为d=2a1,解得d=-1,a1=-$\frac{1}{2}$,
可得an=a1+(n-1)d=-$\frac{1}{2}$-(n-1)=-$\frac{2n-1}{2}$,
即有$\frac{1}{(2n+1){a}_{n}}$=-$\frac{2}{(2n-1)(2n+1)}$=-($\frac{1}{2n-1}$-$\frac{1}{2n+1}$),
则前n项和Tn=-(1-$\frac{1}{3}$+$\frac{1}{3}$-$\frac{1}{5}$+…+$\frac{1}{2n-1}$-$\frac{1}{2n+1}$)
=-(1-$\frac{1}{2n+1}$)=-$\frac{2n}{2n+1}$.
故选:C.
点评 本题考查等差数列的通项公式和求和公式的运用,以及数列的求和方法:裂项相消求和,考查化简整理的运算能力,属于中档题.


 出彩同步大试卷系列答案
出彩同步大试卷系列答案科目:高中数学 来源: 题型:解答题
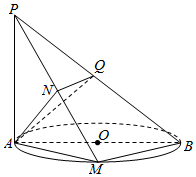 如图,AB为⊙O的直径,PA垂直于⊙O所在的平面,M为圆周上任意一点,AN⊥PM,N为垂足.
如图,AB为⊙O的直径,PA垂直于⊙O所在的平面,M为圆周上任意一点,AN⊥PM,N为垂足.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (ln2,+∞) | B. | (2ln2,+∞) | C. | (-∞,ln2) | D. | (-∞,2ln2) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ①② | B. | ①②③ | C. | ②③④ | D. | ①②③④ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com