练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    8．函数f（x）=$\frac{x}{\sqrt{1-{x}^{2}}}$的导函数为$\frac{\sqrt{1-{x}^{2}}}{（1-{x}^{2}）^{2}}$．

    分析 直接根据导数的运算法则求导即可．

    解答 解：f′（x）=$\frac{\sqrt{1-{x}^{2}}-x（\sqrt{1-{x}^{2}}）′}{1-{x}^{2}}$=$\frac{\sqrt{1-{x}^{2}}-x•\frac{1}{2}（1-{x}^{2}）^{-\frac{1}{2}}（-2x）}{1-{x}^{2}}$=$\frac{1}{（1-{x}^{2}）\sqrt{1-{x}^{2}}}$=$\frac{\sqrt{1-{x}^{2}}}{（1-{x}^{2}）^{2}}$，
    故答案为：$\frac{\sqrt{1-{x}^{2}}}{（1-{x}^{2}）^{2}}$

    点评 本题考查了导数的运算法则，属于基础题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

    18．方程log22x-log2（4x2）+a=0有两个不等的实根，求a的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

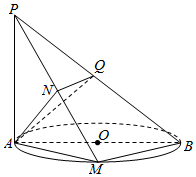    19．如图，AB为⊙O的直径，PA垂直于⊙O所在的平面，M为圆周上任意一点，AN⊥PM，N为垂足．
    （1）求证：AN⊥平面PBM；
    （2）若AQ⊥PB，垂足为Q，求证：NQ⊥PB．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    16．已知m是n的充分条件，m是s的充要条件，则n是s的什么条件？

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    3．已知$\overrightarrow{a}$=1，|$\overrightarrow{a}$-2$\overrightarrow{b}$|=$\sqrt{13}$，$\overrightarrow{a}$与$\overrightarrow{b}$的夹角是60°．
    （1）求|$\overrightarrow{b}$|，|$\overrightarrow{a}$+2$\overrightarrow{b}$|；
    （2）若（$\overrightarrow{a}$+2$\overrightarrow{b}$）⊥（λ$\overrightarrow{a}$-$\overrightarrow{b}$），求实数λ的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

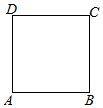    13．如图，四边形ABCD是边长为2的正方形，若点P在正方形内（不含边界），且满足$\overrightarrow{PA}$$•\overrightarrow{PB}$=1
    （Ⅰ）求动点P的轨迹方程；
    （Ⅱ）求|$\overrightarrow{PA}$+2$\overrightarrow{PB}$|的取值范围；
    （Ⅲ）求|$\overrightarrow{PC}$-2$\overrightarrow{PD}$|2的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    6．有两个函数$f（x）=asin（kx+\frac{π}{3}），g（x）=btan（kx-\frac{π}{4}）（k＞0）$，它们的最小正周期之和为3π，且满足$f（2π）=g（\frac{π}{2}），f（\frac{3π}{2}）=g（\frac{5π}{12}）-2$，求这两个函数的解析式，并求g（x）的对称中心坐标及单调区间．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    3．若复数z满足（z-1）i=1+i，则复数z的虚部为（　　）
    A．-iB．1C．-1D．i

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    4．已知函数f（x）在R上的导函数为f′（x），若f（x）＜2f′（x）恒成立，且f（ln4）=2，则不等式f（x）＞e${\;}^{\frac{x}{2}}$的解集是（　　）
    A．（ln2，+∞）B．（2ln2，+∞）C．（-∞，ln2）D．（-∞，2ln2）

    查看答案和解析>>

    同步练习册答案